Дано: AB = 12см
BC = 13см
AC = 20см
A₁B₁ = 9см
Найти: B₁C₁
A₁C₁
По третьему признаку подобия треугольников: Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то они подобны.
Если \frac{AB}{A_1B_1}= \frac{BC}{B_1C_1}=\frac{AC}{A_1C_1}
A
1
B
1
AB
=
B
1
C
1
BC
=
A
1
C
1
AC
, то Δ ABC ~ Δ A₁B₁C₁
Подставим значения сторон треугольника, которые уже знаем
\begin{gathered}\frac{12}{9}= \frac{13}{B_1C_1}=\frac{20}{A_1C_1}frac{4}{3}= \frac{13}{B_1C_1}=\frac{20}{A_1C_1}\end{gathered}
9
12
=
B
1
C
1
13
=
A
1
C
1
20
3
4
=
B
1
C
1
13
=
A
1
C
1
20
Теперь найдём стороны B₁C₁ и A₁C₁
B_1C_1=13:\frac{4}{3}=13*\frac{3}{4}=\frac{39}{4}=9\frac{3}{4}=9,75B
1
C
1
=13:
3
4
=13∗
4
3
=
4
39
=9
4
3
=9,75
A_1C_1=20:\frac{4}{3}=20*\frac{3}{4}=\frac{60}{4}=15A
1
C
1
=20:
3
4
=20∗
4
3
=
4
60
=15
ответ: A₁B₁ = 9см
B₁C₁ = 9,75см
A₁C₁ = 15см
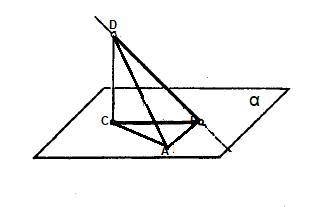
Из точки D, не принадлежащей плоскости α, проведены к этой плоскости перпендикуляр DC и две равные наклонные DA и DB. Известно, что наклонные равны 4 см и ∠CDB=32°. Найдите перпендикуляр DC и проекцию наклонной AC.
Объяснение:
DC-перпендикуляр к плоскости , DA и DB-наклонные, DA=DB=4 см, CA-проекция наклонной DA.
1)ΔDСВ-прямоугольный , т.к. DC⊥α ( значит любой прямой лежащий в этой плоскости)
cos∠CDB=DС/DВ , cos32°=DС/4 ,DС=4cos32° ;
sin∠CDB=CВ/DВ , sin32°=CВ/4 , СВ=4sin32°.
2)ΔDAC=ΔDBC как прямоугольные по катету и гипотенузе:
катет DC-общий, гипотенузы DA=DB поусловию⇒CA=CD=4sin32°.
x1=-4; x2=2
Объяснение:
подставляем в уравнение y=5;
5=x*x+2*x-3
x*x+2x-8=0
решаем квадратное уравнение;
x1=-4; x2=2
Т.е. функция имеет значение 5 при двух значениях x
x1=-4; x2=2