Заданное уравнение x^2+3x+y=0 определяет параболу (λ2 = 0)
Выделяем полные квадраты:
(x^2+2·(3/2)x + (3/2)^2) -1·(3/2)^2 = (x+(3/2))^2-(9/4 ).
Преобразуем исходное уравнение:
(x+(3/2))^2 = -y + (9/4).
Получили уравнение параболы:
(x - x0)2 = 2p(y - y0) .
(x-(-3/2))^2 = 2·(-1/2)(y - (9/4) ).
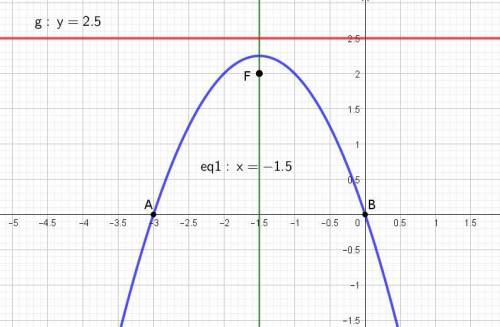
Ветви параболы направлены вниз (p<0), вершина расположена в точке (x0, y0), т.е. в точке (-3/2; (9/4) ).
Параметр p = -1/2
Координаты фокуса: F((-3/2); 2).
Уравнение директрисы: y = y0 - (p/2 )
y = (9/4) - (-1/4) = 5/2
Детальнее параметры кривой даны во вложении.

Для простоты записи пусть точки обозначены:
A(9; 5; 5), B(-3; 7; 1), C(5; 7; 8), D(6; 9; 2).
а) Для получения уравнения плоскости ABC нужно найти смешанное произведение векторов AB и AC.
Для составления уравнения плоскости используем формулу:
x - xA y - yA z - zA
xB - xA yB - yA zB - zA
xC - xA yC - yA zC - zA = 0
Подставим данные и упростим выражение:
x - 9 y - 5 z - 5
-3 - 9 7 - 5 1 - 5
5 - 9 7 - 5 8 - 5 = 0
x - 9 y - 5 z - 5 | x - 9 y - 5
-12 2 -4 | -12 2
-4 2 3 | -4 2 =
6(x - 9) + 16(y - 5) - 24(z - 5) + 36(y - 5) + 8 (x - 9) + 8(z - 5) =
= 6x - 54 + 16y - 80 - 24z + 120 + 36y - 180 + 8x - 72 + 8z - 40 =
= 14x + 52y - 16z - 306 = 0 или, сократив на 2:
7x + 26y - 8z - 153 = 0.
Подсчёт произведен методом "косых полосок".
б) Находим вектор АВ: (-3-9; 7-5; 1-5) = (-12; 2; -4).
Уравнение АВ: (x - 9)/(-12) = (y - 5)/2 = (z - 5)/(-4).
в) Нормальный вектор DM определяем из уравнения плоскости АВС.
DN = (7; 26; -8) - он будет направляющим вектором DM.
Если известна некоторая точка пространства (примем точку D), принадлежащая прямой, и направляющий вектор данной прямой, то канонические уравнения этой прямой выражаются формулами:
( (x - 6)/7) = ((y - 9)/26) = ((z - 20/(-8).
г) Направляющий вектор заданной прямой CN, параллельной АВ, будет равен направляющему вектору АВ: (-12; 2; -4).
Подставляем координаты точки С:
Уравнение CN: (x - 5)/(-12) = (y - 7)/2 = (z - 8)/(-4).
Если я правильно поняла, то должен получиться такой ответ.
Объяснение: рассмотрим ACD. По т. о сумме углов треугольника угол ACD равен 30 градусам. Известно, что против угла в 30° лежит катет, равный половине гипотенузы, значит, AC =24. По т. Пифагора находим СD. Она и будет высотой цилиндра.