тебе нужно просто расставить буквы к данной функции.
1. с (применяется правило синуса. противоположный катет к гипотенузе)
2. а (правило косинуса. прилежащий катет к гипотенузе)
3. а (правило синуса)
4. с (правило косинуса)
5. не возможно найти (так как правило противолежащий катет к прилежащему катету, а у нас отношения такого не дано.)
6. в (правило котангенса. прилежащий катет к противолежащему катету )
7.в (правило тангенса. противолежащий катет к прилежащему катету)
8.не возможно найти (так как по правилу прилежащий катет к противолежащему катету, а нам отношение не дано)
вот и все. не забудь построить прямоугольный треугольник и правильно указать буквы.
Рассмотрим треугольники АОD и ВОС, которые образовались в следствие пересечения плоскости отрезком. Они будут подобны, так как их углы равны. Представил АО как Х, тогда ВО будет равно 15-х. Согласно теореме подобия мы делаем выводы:
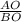 =
= 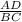 =>
=>  =
=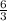
х = 30-2х, отсюда х = 10, следовательно => АО=10, а ВО=5 (15-10).
После этого нам надо найти ОD и ОС по теореме Пифагора, так как треугольники AOD и BOC - прямоугольные:
ОD = √АО²-АD² = √100-36 = 8 сантиметров
ОС = √ВО²-ВС² = √25-9 = 4 сантиметров
Найдем теперь проекцию этого отрезка на плоскость:
CD = OC+ОD = 4+8 = 12 сантиметров
ОТВЕТ: 12 сантиметров
S = 12π ед².
Объяснение:
Проведем высоту ОН в равнобедренном треугольнике OKL.
Высота равнобедренного треугольника - биссектриса и ∠КОН=60°, а ∠ОКН + ∠КОН = 90° по свойству острых углов прямоугольного треугольника КОН).
Тогда в прямоугольном треугольнике ОКН, угол ∠ОКН=30° и
ОК = 2·ОН - по свойству катета против угла 30°.
Перпендикуляр к хорде из центра окружности делит хорду пополам. Значит КН = 3√3.
По Пифагору ОК² = КН² + ОН² => ОК² = (3√3)² + (ОК/2)² =>
ОК = R = 6 ед.
Площадь круга равна S = πR² = 36π.
Площадь сектора круга (заштрихованной части) по формуле равна
Sc = πR²·α/360°.
В нашем случае α = 360° -120° =240°. =>
Sc = π·36·120/360° = 12π ед².