Тема: "окружающая среда"
* * * для удобства плоскость (ABCD) обозначаем через Ψ * * *
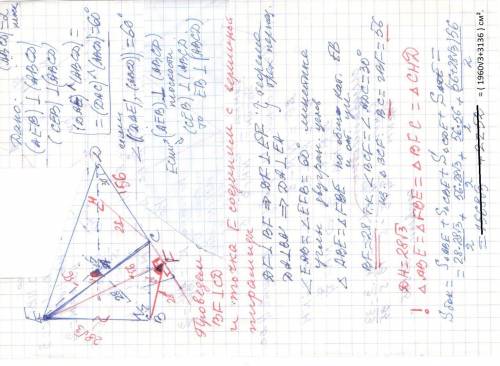
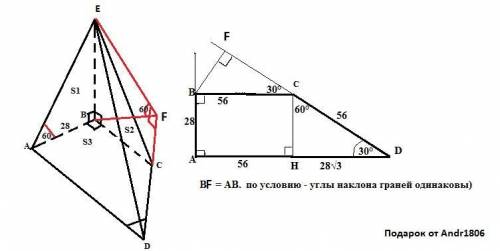
EABCD - пирамида , основание которой трапеция ABCD ;
AD || BC ; AB =28 ; ∠A =∠B =90° ; ∠D =30° ; | [AB] < [CD] ; [BC] < [AD]
(ABE) ⊥ Ψ и (CBE) ⊥ Ψ ; ∠ ( (CDE) , Ψ ) =∠ ( (ADE) , Ψ ) = 60°
--------------------------
1. Трапеция ABCD ПРЯМОУГОЛЬНАЯ
- - -
(ABE) ⊥ Ψ и (CBE) ⊥ Ψ ⇒ EB ⊥ Ψ
DA⊥ BA ⇒DA ⊥ EA ; ∠EAB =60° линейный угол двугранного угла
EADC ; Построим линейный угол двугранного угла EDCA
Проведем BF ⊥ CD и основание F этого перпендикуляра соединим с вершиной ПИРАМИДЫ E. Получаем ∠EFB = 60° линейный угол двугранного угла EDCA .
* * * ! ΔABE = ΔFBE =Δ BFC = ΔCHD учитывая ∠D =∠BCF =30° * * *
Вычисление площадей боковых граней и т.д. cм приложение
Даны точки M(0;1;1), N(2;-1;3), K(-1;y;0).
1. Найдите такое значение y, чтобы выполнялось условие:|MK|=|NK|.
|MK| = √((-1-0)²+(y-1)²+(0-1)²) = √(y²-2y+3)
|NK| = √((-1-2)²+(y-(-1))²+(0-3)²) = √(y²+2y+19)
Возведем оба значения в квадрат и приравняем.
y²-2y+3 = y²+2y+19 => y=-4.
2.Найдите координаты точки,лежащей на оси y и равноудаленной от точек P(4;-1;3) и Q(1;3;0).
Искомая точка R(0;y;0). Тогда |PR|=|QR|.
|PR|=√((0-4)²+(y-(-1))²+(0-3)²) = √(y²+2y+26).
|QR|=√((0-1)²+(y-3)²+(0-0)²) = √(y²-6y+10).
y²+2y+26 = y²-6y+10 => y = -2.
ответ: R(0;-2;0)
3. Найдите координаты точки, лежащей в плоскости xy и равноудаленной от точек A(0;1;0), B(-1;0;1), C(0;-1;0).
Искомая точка D(x;y;0), а равные расстояния от нее до точек А,В и С, - это модули векторов AD, BD и CD.
|AD|=√((x-0)²+(y-1)²+(0-0)²) = √(x²+y²-2y+1). (1)
|BD|=√((x-(-1))²+(y-0)²+(0-1)²) = √(x²+2x+y²+2). (2)
|CD|=√((x-0)²+(y-(-1))²+(0-0)²) = √(x²+y²+2y+1). (3)
Приравняем квадраты выражений (1) и (3):
x²+y²-2y+1 = x²+y²+2y+1 => y=0.
Подставим это значение в (1) и (2): x²+1 = x²+2x+2 =>
x= -(1/2). Итак, получили точку D(-1/2;0;0).
Проверим:
|AD|=√(1/4+1+0) = √5/2.
|BD|=√(1/4+0+1) = √5/2.
|CD|=√(1/4+1+0) = √5/2.
На фото решение, я из 7 класса, так что решение тоже так, как обучали нас)