ответ: во вложении Объяснение:



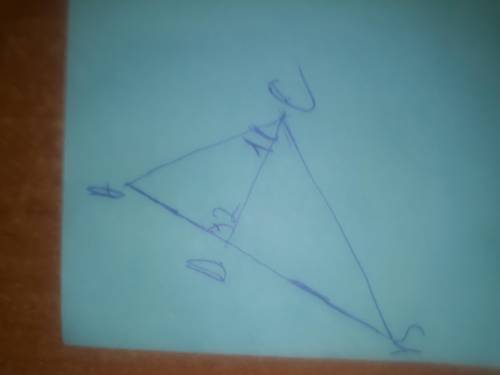
1)дано треугольник АВС, АВ>АС
Доказать: угол С>угла В
Решение:отложим на стороне АВ отрезок AD=AC
Так как AD<AB,то D лежии между А и В.
Следовательно угол 1 является частью угла С и, значит угол С> угла 1.
Угол 2-внешний угол треугольникa BDC, поэтому угол 2> угла B
Угол 1 и угол 2 между собой равны (треугольник ADC-равнобедренный)
Угол С> угол 1, угол 1=угол 2, угол 2>угол В следовательно угол С>угол В.
2) первый признак: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника,то такие треугольники равны.
Второй признак: если сторона и два прилежащих к ней угла одного треугольника соответственно равны стророне и двум прилежащим к ней углам другого треугольника,то такие треугольники равны.
Третий признак: если три стороны одного треугольника соответственно равны трем сторонам другого треугольника,то такие треугольники равны.
3)пусть боковая сторона равна 5х
Тогда основание равно 2х
Так как треугольник равнобедренный то вторая боковая сторона тоже равна 5х
Отсюда P=5x+2x+5x=48
12x=48
X=4
Основание равно 2х=2×4=8
Боковая сторона 5х=5×4=20
Рисунок к 1 задаче тоже отправил если нужно будет!
Если две прямые на плоскости пересечены секущей, то для их параллельности необходимо и достаточно, чтобы накрест лежащие углы были равны, или соответственные углы были равны, или сумма односторонних углов равнялась 180°.
1) BC || AD
∠BCA = ∠CAD — накрест лежащие
2) a || b
накрест лежащие углы равны, сумма односторонних равна 180°
3) m || n
m и n ⊥ k — они уже являются параллельными, но, к дополнению, равны и соответственные углы и сумма односторонних 180°, т.к. все углы по 90°.
4) MN || KP
∠NOM = ∠KOP как вертикальные ⇒ ΔMNO равен ΔPKO по первому признаку равенства треугольников (две стороны и угол между ними)
Пары углов (∠N = ∠K) и (∠M = ∠P) — как накрест лежащие
5) SR || PT
SR и PT ⊥ SP — они уже являются параллельными, но, к дополнению, ∠S = ∠P = 90°, ∠SMR = ∠PMR как вертикальные ⇒ ΔSRM равен ΔPTM по второму признаку равенства треугольников (сторона и два прилегающих угла) .
∠R = ∠T — как накрест лежащие
6) d || e
равны соответствующие углы (по 40° и 140°), и сумма односторонних равна 180° (140+40).
7) RS || MQ, RM || SQ
отрезок MS — общий для ΔSRM и ΔMQS. Данные треугольники равны по первому признаку равенства треугольников:
∠RSM = ∠QMS — как накрест лежащие при RS || MQ
∠RMS = ∠QSM — как накрест лежащие при RM || SQ
8) m || n
равны соответствующие углы (по 36° и 144°), и сумма односторонних равна 180° (144+36).
9) a || b
равны накрест лежащие углы (по свойству биссектрисы угла и равнобедренного треугольника)
10) PQ || MN, PM || QN
отрезок PN — общий для ΔPQN и ΔNMP. Данные треугольники равны по первому признаку равенства треугольников:
∠QPN = ∠MNP — как накрест лежащие при PQ || MN
∠QNP = ∠MPN — как накрест лежащие при PM || QN
11) BA || DC
∠BEA = ∠CED как вертикальные ⇒ ΔBEA равен ΔCED по первому признаку равенства треугольников (две стороны и угол между ними)
Пары углов (∠EDC = ∠EAB) и (∠EBA = ∠ECD) — как накрест лежащие
12) m || n
равны накрест лежащие углы (по свойству биссектрисы угла и равнобедренного треугольника)
13) MS || FQ
MS — биссектриса ∠NMQ. Угол ∠NMQ — внешний для вершины M равнобедренного треугольника MFQ. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним ⇒ ∠MFQ = ∠MQF = ∠NMS = ∠SMQ.
∠SMQ = ∠MQF — как накрест лежащие
14) BC || AD, BA || CD
Пары углов (∠BOA = ∠DOC) и (∠BOC = ∠DOA) как вертикальные ⇒ ΔBOA равен ΔDOC и ΔBOC = ΔDOA по первому признаку равенства треугольников.
∠OBC = ∠ODA и ∠OCB = ∠OAD — как накрест лежащие при BC || AD
∠OBA = ∠ODC и ∠OAB = ∠OCD — как накрест лежащие при BA || CD