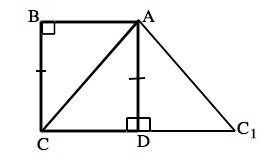
Отложим на продолжении DС в сторону от D отрезок DC1, равный АB. Соединим C1 и А.
В ∆ АDC1 угол АDC=90° (смежный углу АDС). В ∆ АDC1 и ∆ АBС катет DС1=АВ по построению, АD =СВ по условию. ⇒
∆ АDC1=∆ АBС по первому признаку равенства треугольников. .
Значит, АC1=АС, поэтому ∆ АC1С - равнобедренный, АD - его высота и медиана, ⇒ ∆ АDC1=∆ АDС.
Так как ∆ АBС=∆ АDC1( доказано), то ∆ АВС=∆ АDС, ч.т.д.
-------------
Если без подробного доказательства, то по признаку равенства прямоугольных треугольников:
Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.⇒
∆ ABC=∆ CDA
Удаленность т. S от любой из вершин 5 см ( по условию).
Диагональ квадрата = 6 корней из 2. Половинка = 3 корня из 2.
Осталось лишь найти катет SH. (из треугольника SAH либо SBH либо SCH либо SCH , как нравится, в общем, H - точка пересечения диагоналей квадрата).
Я выберу SAH: SA = 5; AH = 3 корня из 2. SH - ?
AH^2 + SH ^ 2 = SA ^ 2
3
ответ: SH =