Задача:
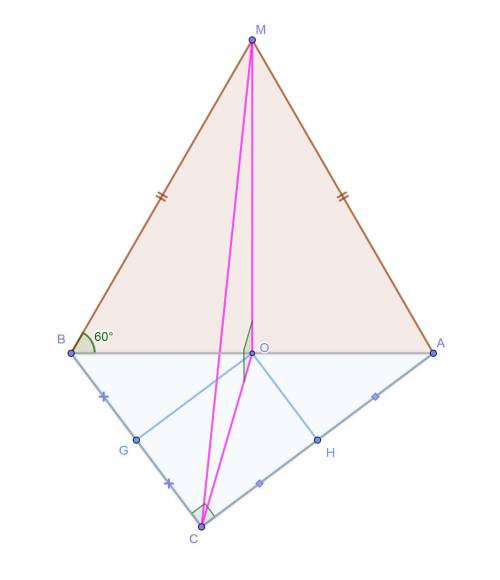
Плоскости прямоугольного треугольника ABC (∠C = 90°) и равнобедренного треугольника ABM (AM=BM) перпендикулярны. Средние линии прямоугольного треугольника, параллельные катетам, равны 6 и 8. Найдите расстояние между точками M и C, если угол наклона отрезка BM плоскости ABC равен 60°.
Пусть отрезок МО — перпендикуляр, опущенный на проскость ABD, пренадлежащий плоскости ACB. Отрезок МС — наклонная.
Р-м ΔABC:
Средняя линия треугольника параллельна основанию и равна его половине. Пусть OH = 6, тогда OG = 8.
BC = OH*2 = 6*2 = 12
AC = OG*2 = 8*2 = 16
AC и BC — катеты прямоугольного треугольника, ищем гипотенузу по т. Пифагора:
AB² = BC²+AC²
AB = √(12²+16²) = √(144+256) = √400 = 20
OC — проекция наклонной MC на плоскость АВС, OC ⊥ AB. Рассмотрев прямоугольный ΔOCH (∠OHC = 90°), ищем длину гипотенузы ОС по т. Пифагора:
OC = √(CH²+OH²) = √(8²+6²) = √(64+36) = √100 = 10
Р-м ΔАВМ:
Углы при основании равнобочного треугольника равны: ∠MBO = ∠OAM = 60°. Не трудно вычислить, что угол вершины М также равен 60°, откуда следует, что ΔАВМ — равносторонний:
AB = BM = MA = 20.
Отрезок МО — перпендикуляр к плоскости АВС и высота, т.к ΔABM равнобедренный.
Рассмотрев прямоугольный ΔBMO (∠BOM = 90°), находим длину отрезка МО (катета) по т. Пифагора:
MО = √(BM²−BO²) = √(20²−10²) = √(400−100) = √300 = √100·√3 = 10√3
Р-м: ΔMOC:
∠MOC = 90°, т.к отрезки МО и ОС принадлежат перпендикулярным плоскостям. Ищем длину гипотенузы МС (она же — расстояние между точкаими М и С) по т. Пифагора:
MC = √(OC²+OM²) = √(10²+(10√3)²) = √(100+100·3) = √400 = 20.
Расстояние между точками М и С равно 20.
Задача:
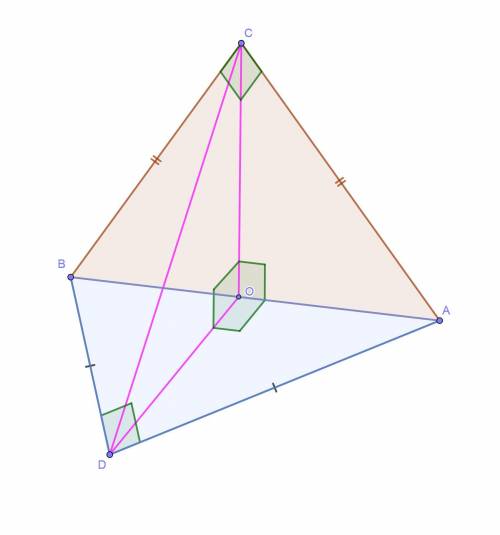
Два равнобедренные прямоугольные треугольника ABC и ABD, которые имеют общую гипотенузу AB, лежат в перпендикулярных плоскостях. Найдите длину отрезка CD, если AB = 8√2.
Пусть отрезок СО, принадлежащий плоскости ABC, — перпендикуляр, опущенный на плоскость ABD. Тогда OD — проекция наклонной CD.
Если одна из сторона равнобедренного прямоугольного треугольника равна стороне другого равнобедренного прямоугольного треугольника, то такие треугольники равны.
Р-м ΔАВС:
АС = СВ. ∠C — вершина, равна 90°. Острые угли равны, т.к треугольник равнобочный. Сумма острых углов равна 90°, значит оба они по 45°. ОС — высота, делящая основу АВ пополам.
AO = OB = (8√2)/2 = 4√2
Р-м ΔАОС:
∠C = 90°, тогда угол АСО = 180−(90+45) = 45°.
Следовательно все углы равны, треугольник равносторонний:
AC = CB = CO = 4√2
Аналогично для ΔABD:
Высота OD делит треугольник на два равных равносторонних со сторонами 4√2.
Р-м ΔCOD:
∠COD = 90°, т.к. отрезки (катеты) принадлежат перпендикулярным плоскостям. Ищем длину отрезка CD (гипотенузы) по т. Пифагора:
CD = √(OC²+OD²) = √((4√2)²+(4√2)²) = √(16·2+16·2) = √64 = 8.
Длина отрезка CD равна 8.
Какой многоугольник не имеет диагоналей?
- - -
ответ : треугольник.
- - -
Почему?
Количество диагоналей многоугольника вычисляется по формуле -
Где N - количество диагоналей многоугольника, n - количество сторон многоугольника.
В нашем случае N = 0. Подставляем в данную формулу это значение и находим чему равно n -
Уравнение имеет два корня. Естественно, что n ≠ 0, так как многоугольника с количеством сторон, равным 0, 1, 2 не существует. То есть n = 0 не удовлетворяет условию. Поэтому, только остаётся, что n = 3.