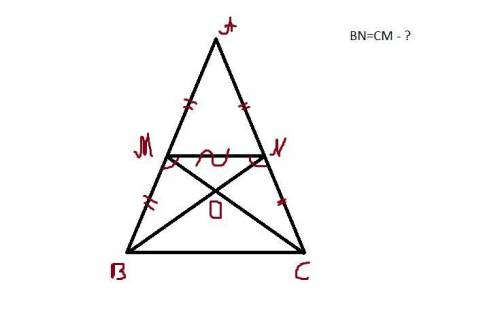
Т.к. АВ=АС , то треугольник равнобедренный
Прямая MN - средняя линия треугольника, значит она разбивает стороны АВ и АС на равные отрезки, которые также равны между собой
Прямая MN отделяет от треугольника АВС равнобокую трапецию BMNC с диагоналями BN и МС. А т.к. трапеция равнобокая, то ее диагонали равны, т.е. BN = МС, ч.т.д.
Или же можно продолжить доказывать равенство этих прямых через ПРТ (треугольники на рассмотрение: BMN и CNM). У них MN - общая сторона; BM=NC и ∠BMN = ∠CNM (как односторонние углы равнобокой трапеции). Отсюда ΔBMN = ΔCNM по 1 ПРТ, значит, BN = МС, ч.т.д.
Пусть одна часть равна х, тогда по условию АМ=3х, МD=2х.
Диагональ ВD делит его на два равных треугольника, площади которых также равны, S(АВD)=S(ВСD)= 30 см².
Высота ВН разделила ΔАВD на два треугольника с одной высотой h.
Определим площадь каждого из этих треугольников.
S(АВН)=0,5·АМ·ВМ=0,5·3х·h=1,5хh.
S(ВМН)=0,5·МD·ВН=0,5·2х·h=хh
Сумма площадей этих треугольников равна площади ΔАВD=30 см².
1,5хh+хh=30,
2,5хh=30,
h=30/2,5х=12/х.
Вычислим площадь ΔАВМ.
S(АВМ)=0,5·АМ·h=0,5·3х·12/х=0,5·3·12=18 см².
ответ: 18 см².