Объяснение:
Начертить прямую произвольной длины.
С циркуля и линейки возвести перпендикуляр, равный данной высоте.
( Это одно из простейших построений, Вы наверняка умеете его делать)
Обозначить основание перпендикуляра Н, а свободный конец - В. Это вершина треугольника.
Раствором циркуля, равным длине одной из сторон, из В, как из центра, провести полуокружность до пересечения с первой прямой.
Точку пересечения обозначить А.
Соединив А и В, получим сторонуАВ.
Точно так же отложить вторую сторону раствором циркуля, равным ее длине.
Обозначить точку пересечения дуги с прямой С и соединить с В.
Можно несколько иначе построить вторую сторону.
От А отложить длину второй известной стороны.
Свободный конец обозначить С.
Соединив С и В, получим сторону ВС.
Треугольник по двум сторонам и высоте построен.
Обозначим хорду АВ. Расстояние от точки до прямой измеряется длиной проведенного к ней перпендикуляра.⇒ перпендикуляр ВЕ=6 см.
Из ∆ АМВ по т.Пифагора катет ВМ=8.
ВК - отрезок секущей и является хордой.
ВК||АЕ по условию.
Проведем диаметр АС.
Диаметр перпендикулярен касательной, следовательно, перпендикулярен и параллельной ей секущей.
АС⊥ВК. Диаметр, перпендикулярный хорде, делит ее пополам. КМ=ВМ.=8.
Диаметр - наибольшая хорда окружности.
Если две хорды окружности пересекаются, то произведение отрезков одной хорды, равно произведению отрезков другой хорды.
АМ•СМ=КМ•МВ
6•СМ=64⇒ СМ=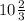 3 см ⇒
3 см ⇒
Диаметр АС=АМ+МС=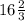 см⇒
см⇒