Объяснение:
Подробно.
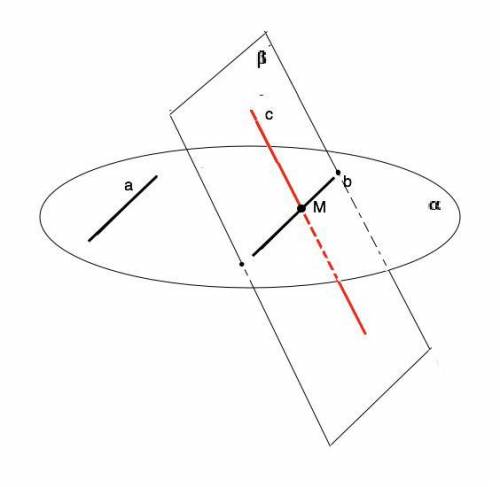
В планиметрии если некая прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую параллельную прямую.
Добавим - при условии, что третья прямая лежит в той же плоскости.
Пусть прямые а и b лежат в плоскости α, а прямая с, не лежащая в этой плоскости, пересекает прямую b в точке M.
Если одна из двух прямых (a) лежит в некоторой плоскости, а другая прямая (с) пересекает эту плоскость в точке (М), не лежащей на этой прямой, то эти прямые скрещивающиеся. Точка М не лежит на прямой а. Прямая с НЕ пересекает прямую а.
Используем одно из основных тригонометрических тождеств: sin^2a+cos^2a=1 (^2 означает двойку в показателе степени, то есть синус в квадрате плюсь косинус в квадрате, тут нельзя писать надстрочными символами) .
Имеем:
sina+cosa=1/2
Возводим в квадрат:
(sina+cosa)^2=1/4
Открываем скобки:
sin^2a+cos^2a+2sinacosa=1/4
Заменяем первые 2 слагаемых значением из формулы в первой строке:
1+2sinacosa=1/4