Объяснение:
Уравнение прямой в параметрической форме удобно для решения систем уравнений, например пересечение прямых.
Каноническая формула прямой Y = k*x + b.
Преобразуем формулу прямой.
6*x - 2*y + 10 = 0
2*y = 6*x +10
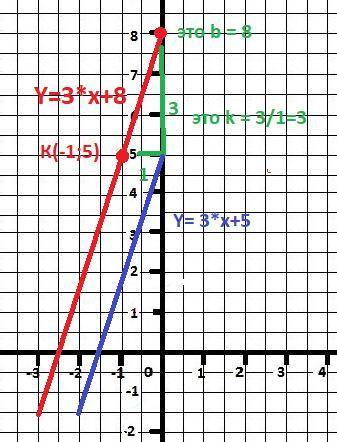
y = 3*x + 5 - каноническая форма записи уравнения.
k = 3 - наклон прямой, b = +5 - сдвиг вверх по оси ОУ при Х =0.
ТЕПЕРЬ надо через точку К с координатой Кх = -1 провести параллельную прямую - под тем де наклоном - k = 3 и имеет высоту Ку = 5.
Ку = k*Kx + b .
5 = 3*(-1) + b
b = 5 + 3 = 8.
ОТВЕТ: y = 3*x + 8 - прямая через точку К.
Дополнительно - рисунок к задаче в приложении.
ответ: ДО=8√3см
Объяснение: обозначим вершины основания пирамиды А В С, вершину пирамиды Д, а её высоту ДО. В основании правильной трёхугольной пирамиды лежит равносторонний треугольник, поэтому АВ=ВС=АС=72м
Найдём площадь основания по формуле:
S=a²√3/4,где а- сторона основания:
S=72²√3/4=5184//√3/4=1296√3см²
S=1296см².
Проведём из вершин основания медианы АН и ВК. Они пересекаясь в точке О делятся между собой в отношении 2:1, начиная от вершины треугольника: АО: ОН=2:1. Также медиана является ещё и высотой, поскольку треугольник равносторонний. Найдём высоту основания через площадь следуя формуле обратной формуле площади:
S=½×a×h
h=S÷a÷½=1296÷72÷½=18×2=36см
h=36см
Обозначим пропорции 2:1 как 2х и х, и зная величину высоты, составим уравнение:
2х+х=36
3х=36
х=36/3
х=12
ОН=12см, тогда АО=12×2=24см.
Рассмотрим ∆АДО. Он прямоугольный где АО и ДО- катеты, а АД- гипотенуза. Угол ДАО=30°, по условиям, а катет лежащий напротив него равен половине гипотенузы, поэтому ДО=½× АД
Пусть ДО=х, тогда АД=2х, зная, что АО=24см, составим уравнение используя теорему Пифагора:
АД²-ДР²=АО²
(2х)²-х²=24²
4х²-х²=576
3х²=576
х²=576/3
х²=192
х=√192=√(3×64)=8√3
Итак: ДО=8√3см