Дано:
AB ∩ CD
∠1 + ∠2 + ∠3 = 297˚.
Найти:
Все неразвёрнутые углы.
__________________________________
Мы знаем точно, что два угла из трёх - вертикальные, а значит между собой они равны.
Пусть x° равны ∠1 и ∠3, тогда ∠2 равен y°. Сумма смежных углов равна 180°, а сумма трёх данных углов - 297°.
Составляем систему уравнений:
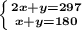
Работа с системой уравнения:
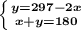
__________________________________
x + (297 - 2x) = 180
x + 297 - 2x = 180
- x = - 117
x = 117
117˚ - ∠1.
НО: Так как прямые образуют вертикальные углы ⇒ ∠1 = ∠3, по свойству.
=> ∠3 = ∠4, тоже по свойству.
∠3 = 297 - (117 + 117) = 63° - ∠3 и ∠4.
Сумма всех 4 углов равна 360°.
ответ: 117˚; 117˚; 63˚; 63˚.
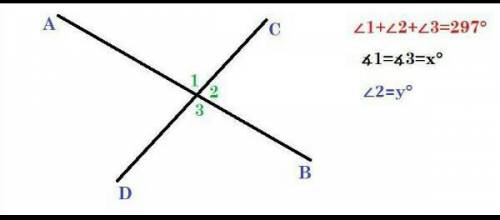
Дано:
AB ∩ CD
∠1 + ∠2 + ∠3 = 297˚.
Найти:
Все неразвёрнутые углы.
__________________________________
Мы знаем точно, что два угла из трёх - вертикальные, а значит между собой они равны.
Пусть x° равны ∠1 и ∠3, тогда ∠2 равен y°. Сумма смежных углов равна 180°, а сумма трёх данных углов - 297°.
Составляем систему уравнений:
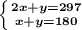
Работа с системой уравнения:
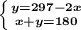
__________________________________
x + (297 - 2x) = 180
x + 297 - 2x = 180
- x = - 117
x = 117
117˚ - ∠1.
НО: Так как прямые образуют вертикальные углы ⇒ ∠1 = ∠3, по свойству.
=> ∠2 = ∠4, как вертикальные.
297 - (117 + 117) = 63° - ∠2 и ∠4.
Сумма всех 4 углов равна 360°.
ответ: 117˚; 117˚; 63°; 63°.
обозначим пирамиду SABCD, где S-вершина.
рассмотрим треугольник DSC.
угол S=60, значит угол D=С=(180-60)/2.
проведем перпендикуляр SE к стороне CD.
т.к. DSC равносторонний, то ES делит сторону DC и угол S пополам.
найдем DE=2/2=1.
найдем угол DSE=60/2=30.
т.к. треугольник DES - равнобедренный, а угол S в нем=30, то по какой-то там теореме катет, лежащий против угла в 30 градусов, в 2 раза меньше гипотенузы этого треугольника.
т.е. DS=DE*2=2.
ВСЁ!)