S1 ≈ 19,8 cм².
S2 ≈ 3,9 cм².
Объяснение:
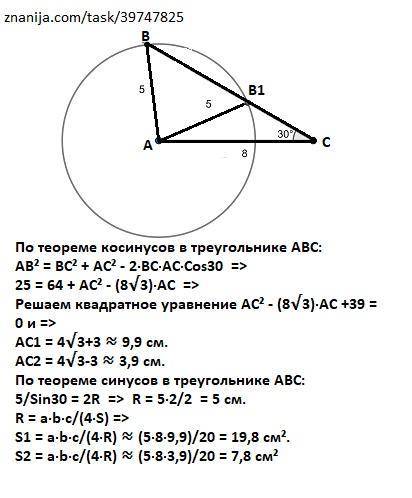
По теореме косинусов в треугольнике АВС:
АВ² = ВС² + АС² - 2·ВС·АС·Сos30 =>
25 = 64 + AC² - (8√3)·AC =>
Решаем квадратное уравнение AC² - (8√3)·AC +39 = 0 и =>
AC1 = 4√3+3 ≈ 9,9 см.
АС2 = 4√3-3 ≈ 3,9 см.
По теореме синусов в треугольнике АВС:
5/Sin30 = 2R => R = 5·2/2 = 5 см.
R = a·b·c/(4·S) =>
S1 = a·b·c/(4·R) ≈ (5·8·9,9)/20 = 19,8 cм².
S2 = a·b·c/(4·R) ≈ (5·8·3,9)/20 = 7,8 cм²
P.S. Для проверки на рисунке выполнено точное построение, доказывающее, что задача имеет два решения.
a) 84*, 84*, 96*, 96*.
б) 62,5*, 62,5*, 117,5*, 117,5*.
в) 71*, 71*, 109*, 109*.
Объяснение
Известно, что в параллелограмме противоположные углы и стороны равны.
a) Значит ∠А=∠С=84* и ∠В=∠D= (360*-2*84)/2=96*
б) ∠A-∠B=55*. Следовательно ∠A=∠B+55*.
Обозначим угол В через х, тогда угол А=х+55
Сумма углов в четырехугольнике равна 360*. Составим уравнение:
(х+х+55)*2=360;
4x+110=360;
4x=250;
x=62,5 - угол В;
Угол А=62,5+55=117,5*
в) Поправка: так как ∠А=∠С, то их разность не может быть 142*. Думаю, здесь закралась ошибка и "не минус", а "плюс". Тогда решаемо:
∠А+∠С=142* и ∠А=∠С=142/2=71*;
∠В=∠D=(360-142)/2=109*.
У Вас может быть как х+14, так и х-14, это будет зависеть от того, что Вы берете за х.Проверим решение Ваше. 13+13+17+17=26+34=60 Периметр не равен 80. Значит, ищите ошибку. Я предлагаю Вам два случая решения.
1 случай. Пусть х- меньшая сторона, тогда смежная ей х+14, полупериметр равен 80/2=40 - это сумма двух смежных сторон. Решим такое уравнение х+х+14=40, 2х=40-14, 2х=26⇒х=13, значит, меньшая сторона 13 см, а большая 13+14=27/см/, я думаю, Вы уже нашли свою ошибку. Подсказка тут не уместна.
Значит, ответ 13см, 13см, 27см, 27см.
2 случай. х- большая сторона, тогда смежная ей меньшая равна х-14, х+х-14=40, откуда 2х=54, х=27, значит, большая сторона равна 27 см, а меньшая 27-14=13/см/
ответ 13см, 13см, 27см, 27 см.