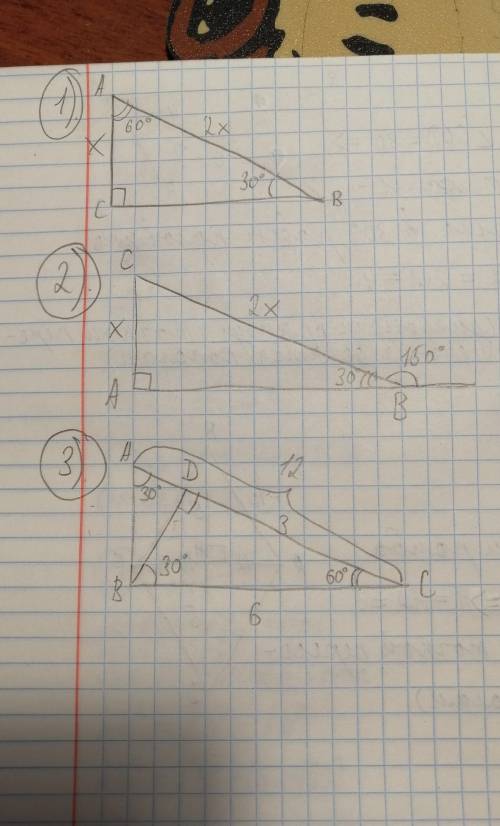
1). угол А = 90° - 30° = 60° => АВ - меньший катет (против меньшего угла меньшая сторона)
т. к. угол В = 30° => АС = 1/2 АВ (катет, лежащий против угла в 30°, равен половине гипотенузы)
Пусть АС = х, тогда АВ =2х
х+2х=36
3х=36
х=12, АВ=2*12=24
ответ: 12, 24
2). Угол СВА = 180°-150°=30° (сумма смежных углов равна 180°) => АС = 1/2 ВС (катет, лежащий против угла в 30°, равен половине гипотенузы)
Пусть АС = х, тогда СВ=2х
2х-х=10
х=10, СВ=2*10=20
ответ: 10, 20
3). Угол А = 30° => ВС = 1/2 АС = 6
Угол С = 90°-30°=60°
треуг. DBC - прямоуг., угол DВС = 90°-60°=30° => CD = 1/2 BC = 3
AD = 12-3=9
ответ: 3, 9
Два решения
1)
Из треугольников ABC, ACD соответственно по теор синусов
CAB=a
CAD=b
BC/sina=AC/sin(a+2b)
CD/sinb=AC/sin(2b+a)
но BC=CD , тогда
sina/sin(a+2b) = sinb/sin(b+2a)
sina*sin(b+2a) - sinb*sin(a+2b) = 0
cos(a-b-2a)-cos(b+3a) - cos(b-a-2b)+cos(a+3b)=0
cos(a+3b)=cos(b+3a)
a+3b=b+3a
2b=2a
a=b
CAB=CAD
2)
Пусть AECF точка O пересечения диагоналей и OE=OF рассмотрим симметрию относительно точки O, точка Е перейдет в точку F, точка B в точку D по определению симметрии так как CB=CD точка А перейдет в себя, тогда AB=AD тогда треугольники ABC=ACD откуда
180-2a-b=180-2b-a
3a=3b
a=b
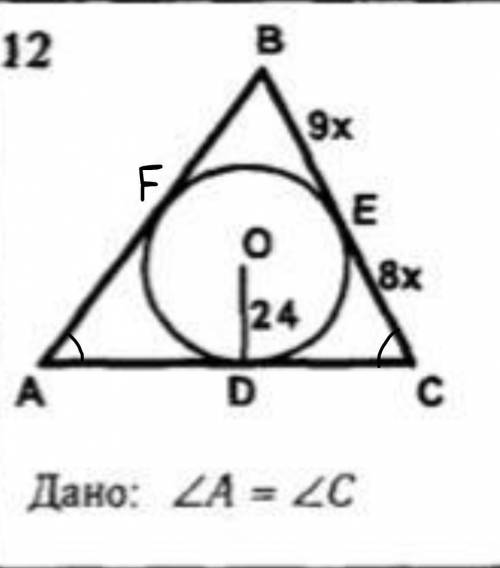
Дано:
В ∆АВС вписана окружность,
F, E, D – точки касания,
∠А=∠С,
OD – радиус вписанной окружности,
ОD=24
BE=9x,
EC=8x.
Так как ∠ВАС=∠ВСА, то ∆АВС – равнобедренный с основанием АС. Значит ВА=ВС.
ВС=ВЕ+ЕС=9х+8х=17х, тогда ВА=17х также.
Отрезки касательных, проведённых из одной точки к окружности, равны. Следовательно:
BF=BE=9x, CD=CE=8x.
AF=BA–BF=17x–9x=8x
АС=AD+CD=8x+8x=16x.
Радиус вписанной в треугольник окружности можно найти по формуле:
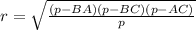
где р – полупериметр треугольника.
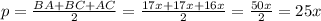
Радиус OD вписанной окружности известен из условия. Подставим все известные значения в формулу:
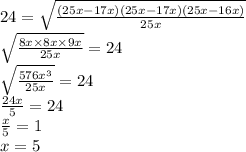
Площадь треугольника равна произведению радиуса вписанной окружности и полупериметра треугольника.
p=25x=5*25=125.
OD=24 по условию
S=OD*p=24*125=3000.
ответ: 3000
ответ: 1) 12√3; 12; 24
2)10; 20
3)3; 9
Объяснение: