1)Из некоторой точки проведены к данной плоскости перпендикуляр, равный 7 см, и наклонная; угол между ними равен 45о. Найти длину проекции наклонной
5 см
7 см
14 см
21 см
10 см
2)Из точки к плоскости проведены две наклонные, равные 10 см и 17 см. Найти длины проекций наклонных, если одна из них на 9 см больше другой
14 см и 8 см
7 см и 10 см
4 см и 11 см
6 см и 15 см
10 см и 15 см
3)Прямые АВ, АС, АД попарно перпендикулярны. Найти отрезок СД, если ВД=9м, ВС=16м, АД=5м
10 м
15 м
13 м
12 м
14 м
4)Дана плоскость, из некоторой точки проведены к этой плоскости две наклонные 6,5 см и 7 см. Проекция второй их них на плоскость равна 3 см. Найти проекцию первой наклонной
6 см
2,5 см
4 см
5,5 см
6,5 см
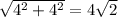 см
см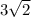
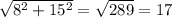 см.
см.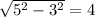 см.
см.
Для начала найдем неизвестные угол и стороны ∆ АКЕ. Сумма углов треугольника 180° => угол КАЕ=180°-(54°+60°=66°
По т.синусов АЕ=АК•sin54°/sin60°. KE=AK•sin66°/sin60°
sin60°=0.8660; sin54°= 0.8090; sin66°=0.9135
AE=20•0,8090/0,8660=18,683≈18,7 см; KE=20•0,9135/0,8660=21,097≈ 21,1 см
Стороны и углы треугольника ВСD имеют те же значения, что и соответствующие углы и стороны ∆ АКЕ, но в условии не указано, какие именно элементы двух треугольников равны. Если в ∆ ВСD сторона ВС=АК, и ∠D=∠Е, то ∠В=∠А=66°,∠С=∠К=54°, ВС=20 см, ВD=AE≈18,7= см, CD=KE≈21,1 см