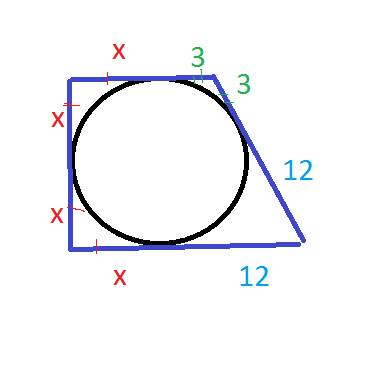
Точка касания с гипотенузой ВС является точка Е (СЕ=2, ВЕ=3), с катетом АС точка К, с катетом АВ точка М. Угол А прямой.
СЕ=СК=2, длины отрезков выходящих из одной вершины до точек касания к окружности равны, по этому же правилу
ВЕ=ВМ=3
Центр окружности О, r-радиус окружности. ОК=ОМ=r и ОК перепендик АС, ОМ перпендик АВ. АМОК-квадрат и АМ=АК=r
Тогда АС=r+2, АВ=r+3, ВС=2+3=5 по теореме Пифагора
ВС^2=АС^2+АВ^2
5^2=(r+2)^2+(r+3)^2
r^2+4r+4+ r^2+6r+9=25
2r^2+10r+13=25
2r^2+10r-12=0 сократим все на 2
r^2+5r-6=0
найдем дискрим. Д=25+24=49
корень из Д=7
r1=(-5+7)/2
r1=1
r2=(-5-7)/2=-6(радиус не может быть отрицательным)
Радиус вписан.окружности равен r=1см
AB=24/sin60=16*sqrt(3), AB=BD, угол ABD=120гр. пО ТЕОРЕМЕ КОСИНУСОВ AD^2=AB^2+BD^2-2*AB*BD*cos120=2*AB^2+2*AB^2*cos60=6*256+3*256=9*256
AD=3*16=48
МОЖНО ЕЩЕ ПРОЩЕ.Из точки В опустить перпендикуляр на AD, пусть будет ВК и тогда треуг. ACB=треуг. ABK(по гипетенузе и острому углу) и получим AC=AK=24, тогда AD=48( высота в равнобедр.треуг. является медианой.)