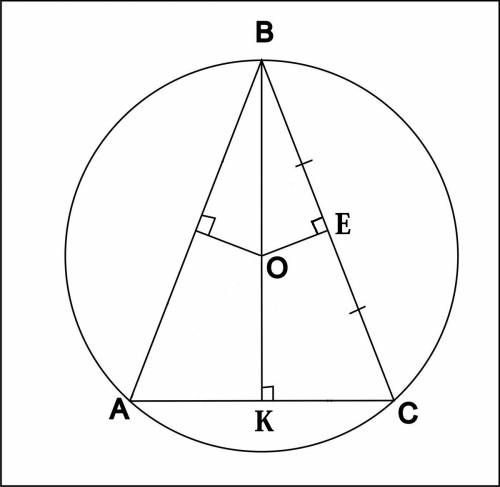
Радиус основания цилиндра равен 13 см, площадь сечения цилиндра плоскостью, параллельной оси цилиндра, равна 80 см², расстояние от плоскости сечения до оси цилиндра равно 12 см. Найдите высоту цилиндра
.
ответ: 8 см
Объяснение:
OA = OD = R = 13 см
Проведем ОН⊥AD. ОН лежит в плоскости основания, АВ - перпендикуляр к плоскости основания, значит ОН⊥АВ.
Тогда ОН⊥(АВС),
ОН = 12 см - расстояние от оси цилиндра до плоскости сечения.
ΔАОН: ∠АНО = 90°, по теореме Пифагора
АН = √(АО² - ОН²) = √(13² - 12²) = √(169 - 144) = √25 = 5 см
ОН - высота равнобедренного треугольника AOD, значит ОН и медиана, ⇒
AD = 2АН = 10 см
ABCD - прямоугольник,
Sabcd = AD · АB = 80
АB = Sabcd : AD = 80 : 10 = 8 см
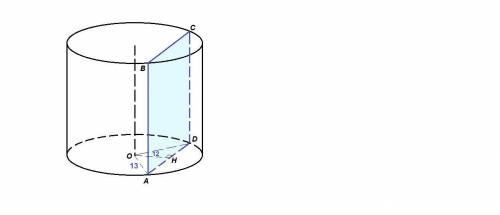
Гипотенузу АВ можем найти по т. Пифагора.
АВ в квадрате = АС в квадрате + ВС в квадрате
АВ в квадрате = 25+75=100
АВ= корень из 100= 10
Угол В можем найти с т. косинусов.
cos В = в числителе - 75+100-25
в знаменателе 2*5 корней из 3*10
cos В= в числителе -корень из 3
в знаменателе 2
так как cos 30 градусов = корень из 3 делённое на 2,значит Угол В равен 30 градусам.