Вообщем я немного упростила это решение
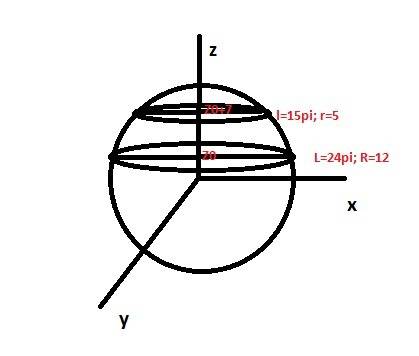
Пусть большее сечение лежит выше центра шара по оси Z , его радиус 12 и центр в точке (0;0;z0)
Тогда его уравнение будет x^2+y^2+z0^2=R^2
Здесь R радиус сферы. Так как радиус большего сечения 12(24pi/2pi), то уравнение большего круга
Будет 12^2+z0^2=R^2
Меньшее сечение x^2+y^2+(z0+7)^2==R^2; 25+z0^2+14z0+47=R^2
Вычитаю из первого второе , получу
119-17z0-49=0
-14z0=-70
Z0=5
Выходит большее сечение находится от центра шара по оси z на расстоянии 5, значит
R^2=5^2+12^2=169
R=13
S(cф)=4pi*13^2=676pi
1) 330√2 м³
2) arccos(5/√299)
Объяснение:
1.Основание любого параллелепипеда это параллелограмм, площадь которого вычисляется как произведение двух его сторон на синус угла между ними.
Sосн=6·11·sin45°=33√2 м²
Объём прямого параллелепипеда равен произведению бокового ребра(равен высоте) на площадь основания.
V=10·33√2=330√2 м³
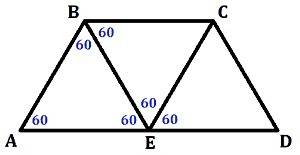
2.Боковые грани правильной четырехугольной пирамиды равнобедренные и равные между собой 4 треугольника, ортогональные проекции которых вместе образуют основание пирамиды. А основание квадрат
Найдём боковую площадь данной пирамиды, которая в 4 раза больше чем площадь одной боковой грани.
По Герону p=0,5(9+9+5)=11,5
S²=p(p-5)(p-9)(p-9)=11,5·6,5·2,5²
(4S)²=16S²=16·11,5·6,5·2,5²=23·13·5²=299·5²
Sбок=4S=5√299
Sосн=5²=25
Пусть угол наклона боковой грани пирамиды к основанию равен α
Sосн=Sбок·cosα⇒cosα=Sосн/Sбок=25/(5√299)=5/√299≈0,0167
α=arccos(5/√299)