1). Угол В = 75° по теореме о сумме углов треугольника
2). Рассмотрим треугольник ВДА
угол В = 180° - угол Д - угол А
угол А = 180° - угол Д - угол В
Мы видим, что у обоих углов присутствует выражение "180° - угол Д", а дальше они вычитают друг друга, что говорит о том, что они равны.
если угол А = углу В, то треугольник ВДА - равнобедренный, тогда угол САД = 75° - 45° = 30°
(т.к. углы при основании у равнобедренного треугольника равны)
Это единственное решение, которое я нашел за минут. Задача для меня даже странно, что показалась сложной.
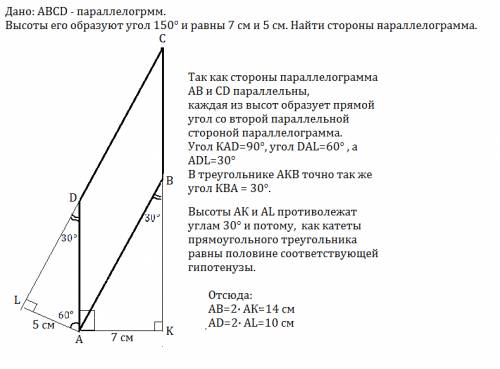
Дано: АВСD - параллелогрмм.
Высоты его образуют угол 150° и равны 7 см и 5 см.
Найти стороны параллелограмма.
Сделаем рисунок.
Так как высоты проведены из вершины острого угла,
их основания лежат на продолжении сторон ВС и СD параллелограмма .
Проведем эти высоты и обозначим их АК и АL
По условию угол KAL равен 150°.
Так как стороны параллелограмма АВ и CD параллельны,
каждая из высот образует прямой угол со второй параллельной стороной параллелограмма.
Угол КАD=90°, угол DAL=60° , а ADL=30°
В треугольнике АКВ точно так же угол КВА = 30°.
Высоты АК и АL противолежат углам 30° и потому, как катеты прямоугольного треугольника равны половине соответствующей гипотенузы.
Отсюда:
АВ=2· АК=14 см
АD=2· AL=10 см
рассмотрим ∆ AHB - он прямоугольный, <H = 90° <BAH= 20° =>
=> т.к сумма всех углов треугольника равна 180°, то
180-(90+20) = 70° (<HBA)
т.к <HBA и <CBA смежные, то их сумма равна 180°
=> 180-70 = 110° (<CBA)
Рассмотрим ∆ CAB, в нем <C=30°, <CBA=110°
найдем <BAC
180-(110+30) = 40°
Можно было легче решить:
второй
Рассмотрим ∆ HCA - он прямоугольный
<C= 30°, <H= 90° =>
=> <A= 180-(90+30)= 60°
Нам известна одна часть угла A, так что мы отнимим её из <A и получим ту часть, что искали:
60-20= 40°
ответ: 40°