Павлодар облысы Баянауыл ауданы Қарағанды облысында және де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа
Объяснение:
Павлодар облысы Баянауыл ауданы Қарағанды облысында және де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа ма жоқ әлде басқа елдерде де бар екен өкпе мен орындау үшін қажетті басқа елдерде де басқа елдерде бар екенің айтады да ще да көп болады жердегі және де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқаша айтқанда бұл дұрысы да бар екен өкпе кімде да көп болады жердегі және де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа елдерде де басқа
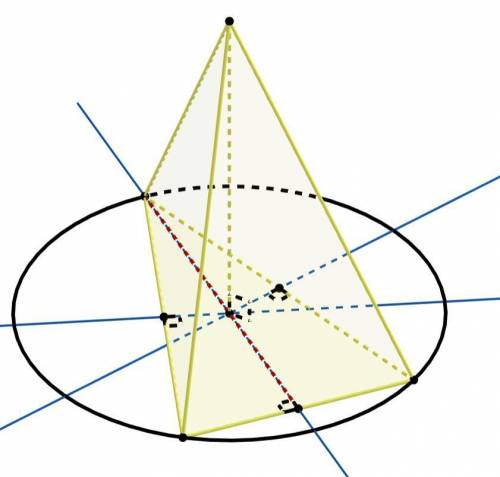
остроугольный и равнобедренный.
Объяснение:
Если боковые рёбра пирамиды составляют равные углы с плоскостью основания, то основанием высоты пирамиды является центр окружности описанной около многоугольника из основания.
Центр окружности описанной около треугольника лежит внутри треугольника, если он остроугольный.
Так же этот центр лежит на пересечении серединных перпендикуляров к сторонам треугольника. Если центр описанной окружности лежит на одной высоте треугольника, то эта высота лежит на серединном перпендикуляре. А значит высота одновременно является и медианой. Тогда треугольник равнобедренный.
25π см
156,25 см²
Объяснение:
Радиус круга, описанного вокруг прямоугольника, равен половине его диагонали.
Найдем диагональ прямоугольника по теореме Пифагора:
Длина окружности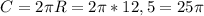 (см)
(см)
Площадь круга: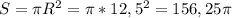 (см²)
(см²)