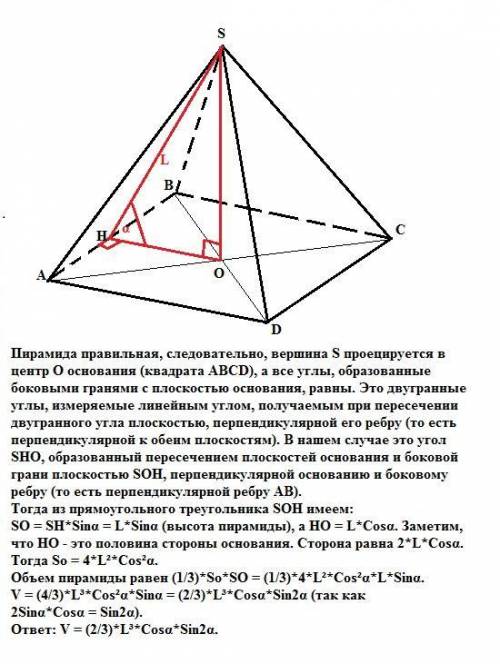
Пирамида правильная, следовательно, вершина S проецируется в центр О основания (квадрата АВСD), а все углы, образованные боковыми гранями с плоскостью основания, равны. Это двугранные углы, измеряемые линейным углом, получаемым при пересечении двугранного угла плоскостью, перпендикулярной его ребру (то есть перпендикулярной к обеим плоскостям). В нашем случае это угол SHO, образованный пересечением плоскостей основания и боковой грани плоскостью SOH, перпендикулярной основанию и боковому ребру (то есть перпендикулярной ребру АВ).
Тогда из прямоугольного треугольника SOH имеем:
SO = SH*Sinα = L*Sinα (высота пирамиды), а НО = L*Соsα.
Заметим, что НО - это половина стороны основания. Сторона равна 2*L*Соsα.
Тогда площадь основания So = 4*L²*Соs²α.
Объем пирамиды равен (1/3)*So*SO = (1/3)*4*L²*Соs²α*L*Sinα.
V = (4/3)*L³*Соs²α*Sinα = (2/3)*L³*Соsα*Sin2α (так как
2Sinα*Cosα = Sin2α).
ответ: V = (2/3)*L³*Соsα*Sin2α.
1)53
2)45;45
4)50
Объяснение:
1)Сумма острых углов прямоугольного треугольника равна 90 градусам. Значит что бы найти один из острых углов надо от 90 отнять известный угол.
2)В равнобедренном прямоугольном треугольнике острые углы одинаковы,значит каждый угол будет по 45°
4)Сумма смежных углов равна 180°. Что бы найти неизвестный смежный угол нужно от 180 отнять известный угол. Из этого мы получаем,что угол СDA равен 110°. Что бы найти угол АСD мы вспоминаем что сумма острых углов в прямоугольном треугольнике равна 90°. От 90 отнимаем 70,получаем 20. Из чертежа мы видим что угол ACD и BCD одинаковы. Значит нужный нам ACD тоже 20°. Далее вспоминаем,что сумма всех углов треугольника равна 180°. От 180 отнимаем сумму двух известных нам углов. 180-(110+20)=50°