Можно ли в плоскости нарисовать n (бесконечно много) углов таким образом, чтобы каждые 142 угл(-ов, -а) имели общую точку, но в то же время можно было найти точку, которая не принадлежит ни одному из n углов?

Да
Нет

В качестве ответа приложи файл с рисунком.
Файл не выбран
Максимальный размер файла: 500 кБ

👇

Открыть все ответы

Ответ:

простоя43

30.03.2020

Радиусом описанной окружности в данном случае будет половина гипотенузы прямоугольного треугольника. Так как вписанный в окружность прямой угол опирается на диаметр этой окружности. Ищем гипотенузу по известной теореме ПифагораAB=16R=AB/2R=8
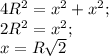
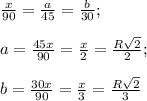
№4Точка С1 симметрична точке С относительно D. Точка М1 (само собой) симметрична точке М относительно AD.
Угол АС1D равен вписанному углу MM1A, опирающемуся на дугу АМ, а дуга АМ равна дуге АМ1. Поэтому угол М1РА равен углу АС1D (или просто углу С треугольника АВC), и треугольники АМ1Р и АС1В подобны (у них все углы равны)
Отсюда AP/AM1 = AC1/AB;
8/6 = x/9;
x = 12;

4,4(95 оценок)

Ответ:

tati9860406

30.03.2020

Возможно, я не правильно поняла Ваши скобки, но у меня получилось такое решение:

Возьмём правильный четырёхугольник, который вписан в данную окружность. Этот четырёхугольник - квадрат, пусть его сторона равна х. Диагональ этого квадрата равна диаметру окружности равна 2R. Тогда получаем через теорему Пифагора следующее утверждение:

$4R^{2}=x^{2}+x^{2}; \\ 2R^{2}=x^{2};\\x= R\sqrt{2}$

Сторона правильного четырёхугольника стягивает дугу в 360\4=90 градусов, тогда сторона восьмиугольника будет стягивать дугу в 360\8=45 градусов, а двенадцатиугольника - 30 градусов. Пусть сторона восьмиугольника равна а, сторона двенадцатиугольника равна б, составим отношение:

$\frac{x}{90} = \frac{a}{45} = \frac{b}{30} ;\\ \\a= \frac{45x}{90} = \frac{x}{2} = \frac{R \sqrt{2} }{2} ;\\\\b= \frac{30x}{90}= \frac{x}{3}= \frac{R \sqrt{2} }{3}$

Возможно, это то, что вам нужно, потому что цифры те же, может быть, вы сможете получить требуемое выражение из этого путём преобразований, но дальше, извините я Вам не в силах, потому что, как уже писала, скобки ваши не поняла.

4,7(46 оценок)

Это интересно:

Компьютеры-и-электроника

03.09.2020

Как стать специалистом в Microsoft Excel: советы от эксперта...

14.02.2020

Как быть честным(ой)?...

Здоровье

15.05.2020

Угревые струпья: как расправиться с ними быстро и эффективно?...

Искусство-и-развлечения

23.04.2020