12
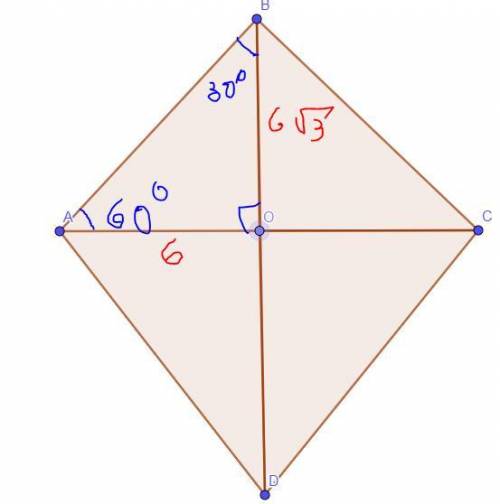
Объяснение:BD - наибольшая диагональ = 12√3.
<A = 120.
1) Посколько диагонали ромба одновременно перпедикулярны (т.е. создают 4 угла по 90°) и являются биссектрисами углов, то меньшая биссектриса AC разбивает <A на 60°.
Из треугольника ABO, нам известно, что <O = 90°. Не сложно найти тогда и <B:
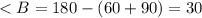 °.
°.
2) DB = 2OB, посколько диагонали ромба точкой сечения делятся пополам, т.е OB = 6√3
Из треугольника ABO найдём сторону AO, лично мне будет удобно использовать теорему синусов, кто-то может использовать тригонометрические соотношения углов, как вам удобно. Итак, имеем:
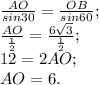
3) AC = 2AO, посколько диагонали ромба точкой сечения делятся пополам, т.е:
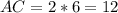 - значения наименьшей диагонали.
- значения наименьшей диагонали.
* * * * * * * * * * * * * * * * * * * * * * *
Дан треугольник ABC, стороны которого равны 10 см., 6 см., 8 см. Является ли прямоугольным треугольник, вершины которого - середины сторон треугольника ABC.
ответ: да
Объяснение:
ΔA₁B₁C₁ ~ ΔABC * * * Третий признак подобия треугольников * * *
( вершины A₁ ,B₁ ,C₁ середины сторон треугольника ABC )
* * * Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине ) .
Треугольник ABC прямоугольный т.к. 10² =6²+8² ( по обратной теореме Пифагора ) ,следовательно ΔA₁B₁C₁ тоже является прямоугольным.
* * * ! треугольник со сторонами 3 , 4 и 5 а также треугольник со строками 3*n ,4*n и 5*n,где n∈N → Пифагорова Δ или Пифагорова тройка * * * ( в данном примере n=2 6=3*2 ; 8=4*2 и 10=5*2 )
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.
Центральный угол=40 градусов
Значит, вписанный угол = 40:2=20градусов