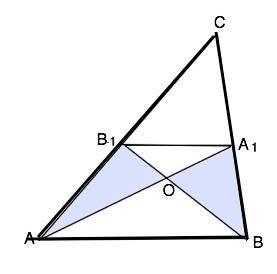
Четырехугольник АВ1А1В - трапеция, В1В и А1А - ее диагонали.
Треугольники, образованные отрезками иагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.( свойство трапеции).
Доказательство.
Рассмотрим ∆ АВ1А1 и ∆ ВВ1А1. У этих треугольников общее основание и высоты, равные высоте трапеции.
Формула площади треугольника S=a•h/2, где а - сторона треугольника, h- высота, проведенная к ней.
Если основания и высоты треугольников равны, их площади равны.
∆ АВ1А1= ∆ АВ1О+∆ В1ОА1
∆ ВВ1А1= ∆ ВОА1+∆ В1ОА1
Два треугольника с равной площадью состоят из частей, одна из которых - одна и та же. Следовательно, площади вторых частей этих треугольников равны.
S ∆ АОВ1=S∆ ВОА1, ч.т.д.
---------
Вариант – более короткое решение.
Каждая медиана треугольника делят его на два равновеликих ( равные высоты и основания).
S∆ ВCВ1=S ∆ АСА1=S ∆ АВС:2
Сумма площадей ∆ АОВ1+четырехугольника В1СА1О равна сумме площадей ∆ ВОА1+четырехугольника В1СА1О, равна половине площади ∆ АВС, из чего следует равенство площадей треугольников АВ1О и А1ВО
a)Треугольник АВМ - равнобедренный ⇒ АВ=ВМ
Треугольник ДМС - равнобедренный ⇒ СД=МС
А так как АВ=СД (как противоположные стороны параллелограмма), то и ВМ=МС.
Значит, если АВ=х, то ВС=2х.
Полупериметр равен 36:2=18 см.
х+2х=18
3х=18
х=6
АВ=СД=6 см
ВС=АД=2·6=12 (см)
ответ. 6 см и 12 см.
b)Проведем высоты ВМ и СН. Так, как меньшая основа будет 6см., а большая 12, и эта трапецыя равобедренная, то ВС=МН, отсюда АМ=НД, ВС=12-6=6см.
НД+АМ=12-6=6см., а значит НД=6/2=3см.
Расмотрим треугольник АВМ, у него: ВМА=90гр., как угол при высоте; ВАМ=60гр., за условием задачи, отсюда угол АВМ=30гр. Значит АМ=1/2*ВА, отсюда ВА=2*АМ=2*3=6см.
ответ:6см.