Уравнение окружности радиусом r с центром в (x0;y0) приведем данной уравнение к такому виду: уравнение прямой, параллельной оси ординат: x=a, где a=const эта прямая проходит через точку с координатами (5;-6), x=5; y=-6 значит: 5=a => a=5 x=5 - искомая прямая центр окружности лежит на оси ox прямая x=5 тоже пересекает ox в точке (5;0) и перпендикулярная ей значит расстояние от центра окружности до прямой x=5 будет перпендикуляр, проведенный из точки (5;0) в точку (-1;0) - он совпадет с ox , значит его длина будет равна модулю разности абсцисс этих точек |5-(-1)|=6 ответ: 6
5. 28
6. 21
Объяснение:
5. АВ = 42, 2BC = AC - это если наше условие написать на математическом языке. Чтобы решить эту задачу, нужно составить уравнение
AC + BC = 42
Но чтобы у нас не было двух неизвестных, нужно один отрезок выразить через другой. Для этого мы и переписали условие
АС + BC = 2BC + BC
2BC + BC = 42
3BC = 42
BC = 42 : 3 = 14
Если BC = 14, то АС = 42 - 14 = 28.
6. АВ = 49, АС =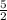 CB или 2,5СВ
CB или 2,5СВ
Чтобы найти АС, мы переписали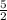 в 2,5 , чтобы проще было посчитать. АС - это две части и одна половинка этой части СВ. То есть,
в 2,5 , чтобы проще было посчитать. АС - это две части и одна половинка этой части СВ. То есть,
СВ + СВ +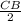 = AC.
= AC.
СВ + СВ +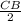 + СВ = 49
+ СВ = 49
3СВ +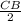 = 49, чтобы легко избавиться от некрасивой дроби, нужно две части уравнения домножить на 2
= 49, чтобы легко избавиться от некрасивой дроби, нужно две части уравнения домножить на 2
6СВ + СВ = 98
7СВ = 98
СВ = 14, следовательно АС = 49 - 14 = 35
Раз нам надо найти АС - СВ, то 35 - 14 = 21.