Решение задач с кругов
Эйлера:
N91. В классе 28 учеников. Каждый
из них начертил у себя в тетради
один из двух четырехугольников -
прямоугольник или ромб. При
проверке прямоугольников
оказалось 17, а ромбов - 15. Как
такое могло случиться?
N92. В осенние каникулы 12
учеников класса участвовали в
междугородных экскурсиях в
Москву и Санкт-Петербург, при этом
8 из них посетили Санкт-Петербург,
6 – Москву. Сколько из этих
учеников побывало и в Москве, и в
Санкт-Петербурге?
решите
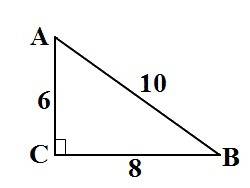
AB - гипотенуза
BC = 8 см - катет
AC - катет
По условию
AB = BC + AC - 4
AB = 8 + AC - 4
AB = AC + 4
По теореме Пифагора:
AB² = BC² + AC²
AB² = 8² + AC²
AB² = AC² + 64
(AC + 4)² = AC² + 64
AC² + 8AC + 16 = AC² + 64
8AC = 64 - 16
8AC = 48
AC = 6 (cм)
Тогда AB = 6 + 4 = 10 (cм)
Получаем прямоугольный треугольник со сторонами 6, 8 и 10.
∠C = 90°
∠A можно определить по синусу угла, т.е. по отношению противолежащего катета BC к гипотенузе AB
sin(A) = BC/AB
sin(A) = 8/10 = 0,8
По таблице Брадиса находим, что данной величине приблизительно соответствует угол 53°7' ≈ 53°
Сумма углов треугольника равна 180° ⇒ ∠B = 180 - 90 - 53 = 37 (°)
∠A является большим из острых углов треугольника ABC.
∠A = 53°
P.S. такой треугольник называется египетским или золотым