1) Если все боковые стороны (это рёбра) пирамиды имеют одинаковую длину, то их проекции на основание - радиусы R описанной окружности вокруг основания.
Радиус равен половине диагонали основания.
R = √(3² + 4²) = 5 см.
Тогда высота Н пирамиды равна:
Н = √(13² - 5²) = √(169 - 25) = 12 см.
2) Будем считать, что в задании имеется в виду, что высота пирамиды проецируется на основание в вершину прямого угла.
Тогда 2 боковых грани пирамиды вертикальны, одна - наклонная.
Гипотенуза основания равна √(9² + 12²) = 15 см.
Высота основания на гипотенузу равна (9*12)/15 = (36/5) = 7,2 см.
Высота наклонной боковой грани равна √(8² + 7,2²) = 0,8√181 ≈ 10,7629 см.
Теперь можно определить площади боковых граней.
Sбок = (1/2) *(6*8 + 12*8 + 15*(4/5)√181) = (72 + 6√181) см².
Площадь основания Sо = (1/2)(9*12) = 54 см².
Полная площади пирамиды равна 54 + 72 + 6√181 = 126 + 6√181 см².
Объём пирамиды равен (1/3)*54*8 = 144 см³.
45°
Объяснение:
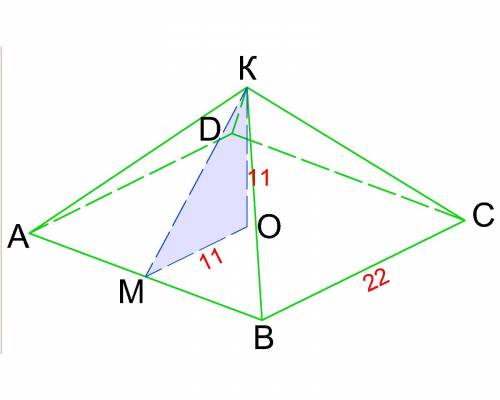
Обозначим основание пирамиды как квадрат АВСД, центр пересечения диагоналей квадрата - т.О, вершина пирамиды - т.К, высота пирамиды - отрезок КО, высота из т.О на сторону АВ основания - отрезок ОМ.
Тогда угол, который образует боковая грань с плоскостью основания будет равен ∠КМО в прямоугольном ΔКМО с катетами ОМ и КО.
Катет КО = 11 см по условию задачи,
катет ОМ равен радиусу вписанной в квадрат основания окружности, поэтому равен половине стороны основания, т.е.
ОМ=22/2=11 см.
Т.к. оба катета равны, то получаем прямоугольный равнобедренный треугольник, с углами при гипотенузе ∠КМО=∠МКО=45°
Отрезок KS - линия пересечения заданных плоскостей.
Проекция апофемы на основание равна радиусу вписанной окружности.
r = OM = 2*cos30° = 2*(√3/2) = √3.
Высота пирамиды Н = √(17 - 2²) = √13.
Отрезок КО равен 2√3.
Длина KS = √(13 + (2√3)²) = √25 = 5.
Из точек М и Р проводим перпендикуляры к KS.
Длина МР как средняя линия трапеции ABEF равна (2 + 4)/2 = 3.
Апофема SM равна √(13 + (√3)²) = √16 = 4.
Отрезки РТ и МТ = 3*sin(MKS) = 3*(4/5) = 12/5.
Искомый угол равен:
α = 2arc sin((3/2)/(12/5) = 2arc sin(5/8) = 77,36437°.