AC=DC ⇒ треугольник ADC равнобедренный
⇒СF биссектриса ∡ACD ⇒ ∡FCD=∡ACF=30°
∡ACD=60°
⇒треугольник ADC равносторонний
Рассмотрим прямоугольный Δ ABF (∡ABF=90°)
⇒СF медиана Δ ADC ⇒AF=4/2=2
∡FAB=60° (равносторонний Δ ADC)
∡AFB=180-(90+60)=180-150=30°
AB=BF/2 (катет лежащий напротив угла 30°)
Пусть BF - x, тогда AB будет 2x
2²+x²=(2x)² (по теореме П.)
4+x²=4x²
x²-4x²= -4
-3x²= -4
3x²=4
x²=4/3
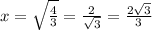
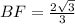
1) 72:12=6см длина ребра куба
2) 6*6=36 см^2 площадь одной грани куба
3)36*6=216 см^2 площадь поверхности куба
4)а+b+c=72:4=18см сумма трех измерений параллелепипеда
3с+2с+с=18
6 с=18
с=3 см
3*2=6 см; 3*3=9 см
3 см; 6 см ; 9см - длина , ширина и высота параллелепипеда
5) 2( ac+ bc+ ab)=2(18+27+54)=198 см^2 площадь поверхности параллелепипеда
6)216-198= на 18 см ^2 площадь поверхности куба больше , чем параллелепипеда
7)6^3=216 см^3 объем куба
8)3*6*9=162 см ^3 объем параллелепипеда
9)216-162 = на 54 см^3 объем куба больше
Вот так? Или я чего то не понял?
ответ:Задание 1
Треугольники АВС и СЕD равны между собой по первому признаку равенства треугольников-если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника,то эти треугольники равны между собой
АС=CD;BC=CE; по условию задачи
Углы АСВ и ЕСD равны между собой,как вертикальные
Равенство треугольников доказано,следовательно соответствующие углы и стороны треугольников тоже равны
Задание 2
Треугольники АВС и АСD равны между собой по первому принципу равенства треугольников
АВ=АD;Углы ВАС и САD равны между собой;
АС-общая сторона
Равенство треугольников доказано,и естественно,равны соответствующие стороны и углы
Объяснение:
АСД равнобедренный
Высота СF медиана и биссектриса.
<ACF=<DCF=30° и AF=FD
CDF: cos30°=CF/CD
CF=CD×cos30°=4корень из 3/2
CBF:BF=1/2CF
BF=1/2×2корень из 3= корень из 3.
-это треугольник. "<" - это угол