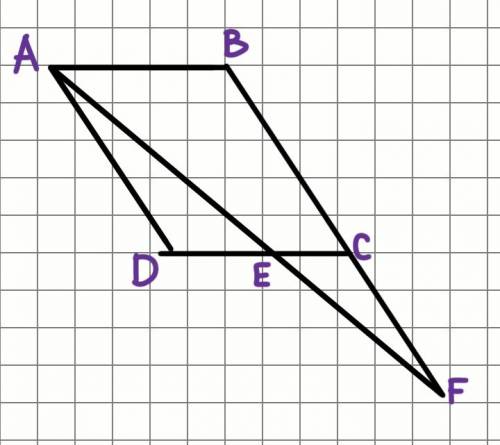
AB и DC параллельны (противоположные стороны параллелограмма).
∠BAF = ∠CEF - соответствующие углы при AB║CD и секущей AF.
∠ABC = ∠ECF - соответствующие углы при AB║CD и секущей BF.
Рассмотрим ΔABF и ΔECF
1. ∠BAF = ∠CEF (из решения)
2. ∠ABC = ∠ECF (из решения)
Отсюда следует, что ΔABF и ΔECF подобны по двум углам.
Найдём коэффициент подобия, он равен отношению подобных сторон треугольников:
k = BF/CF = (56+30)/30 = 86/30 = 43/15
Также из подобия следует, что AB : EC = k
Найдём AB из этой записи:
AB/15 = 43/15
AB = 15*43/15
AB = 43
AB = CD = 43 (так как ABCD параллелограмм)
DE = CD - EC = 43 - 15 = 28
ответ: DE = 28
Назовем соприкосновение наклонной и плоскости точкой А, а соприкосновение плоскости с перпендикуляром В. Рассмотрим треугольник MAB, угол M = 60 градусов по условию, угол B = 90 градусов т.к. "перпендикуляр". Третий угол А по теореме о сумме углов треугольника = 180 - 60 - 90 = 30.
Теперь нам известны все углы и одна сторона MB = 20см, остается "решить треугольник".
Т.к. знаем все углы, воспользуемся теоремой Синусов: MB/sinA = AB/sinM = AM/sinB.
Подставим известное: 20/sin30 = AB/sin60 = AM/sin90. Сдесь 2 неизвестных, по условию нам нужно найти длину наклонной AM. Выразим её из равенства:
AM = sin90*20/sin30
AM = 1*20/0.5 = 20*2 = 40 см.
ответ: 40см
Всего дорог: 24
ответ:20
Объяснение:
Всего дорог: 24
P = (n - 1)!
P = 4!
P = 1 * 2 * 3 * 4 = 24
А теперь посчитаем сколько для скольких дорог не нужны мостики;
1)между А и В
2)между S D
3)между D C
4)между C S
Итого 4.
24 - 4= 20
ответ:20