1200√3 см²
Объяснение:
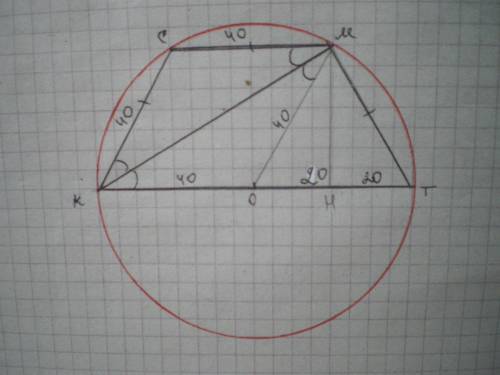
Дано: КСМТ - трапеція, КС=МТ, ∠КМТ=90°, КМ - бісектриса, ОМ=КО=ОТ=40 см. Знайти S(КСМТ).
∠КМТ - прямий, отже він спирається на діаметр описаного кола, тоді КТ=КО+ОТ=80 см.
∠СКМ=∠ТКМ за умовою, ∠СМК=∠ТКМ як внутрішні при СМ║КТ і січній КМ, отже ∠КСМ=∠СКМ, а ΔКСМ - рівнобедрений, КС=СМ.
Проведемо радіус ОМ=40 см, ΔКОМ=ΔКСМ за двома кутами і спільною стороною, отже КС=СМ=КО=ОМ=40 см.
МТ=КС=40 см.
ΔОМТ - рівнобедрений, проведемо МН - висоту і медіану.
ОН=ТН=40:2=20 см
За теоремою Піфагора МН=√(МТ²-ТН²)=√(1600-400)=√1200=20√3 см.
S(КСМТ)=(СМ+КТ):2*МН=(40+80):2*20√3=1200√3 см²
Площадь треугольника = 1/2 х основания на высоту
Высота в равнобедренном треугольнике - медиана, биссектриса. УГОЛ В = 180-30-30=120
Половина угла В =120/2=60
В треугольнике АВН :
ВН - высота = а, и лежит напротив угла 30, значит АВ - гипотенуза = 2а
АН = АВ х cos 30 = 2а х (корень 3/2) = а х (корень 3)
АС = 2 х АН = 2а х корень 3.
Площадь = 1/2 АС х ВН = 1/2 х 2а х (корень 3) х а = а в квадрате х корень 3 = 9 х корень 3 (из условия)
а в квадрате = 9
а=3
высота ВН=3
Гипотенуза АВ = 3 х 2=6
1) ABD=ADC
2) ABD=BCD
3) ABD=ACD , ABE=CDE