вот ссылка видео в ютубе та все написано посмотри
1. Сторона треугольника a= 2Rcos30o.
2. 1) Знайдемо радіус вписаного кола у правильний трикутник:
2) Діагональ вписаного у коло квадрата рівна діаметру цього кола і дорівнює подвоєному радіусу:
3) Сторону квадрату знайдемо за т. Піфагора:
3.
4.В трапецию можно вписать окружность, если сумма противоположных сторон равна. то есть AD+BC=AB+CD
Опустим с вершины B трапеции на основание BK высоту BK, тогда
AK=AD-KD=28-21=7
Пусть высота трапеции BK=x, тогда
(AB)^2=(BK)^2+(AK)^2=x^2+7^2
AB=sqrt(x^2+7^2)
Так как
AD+BC=AB+CD, то
21+28=x+sqrt(x^2+7^2)
sqrt(x^2+7^2)=49-x
x^2+7^2=(49-x)^2
x^2+49=2401-98x+x^2
98x=2352
x=24, то есть высота трапеции равна 24
R=H/2
R=24/2=12 - радиус вписанной окружности
Площадь трапеции равна 900√3 м²
Объяснение:
Дано:
ABCD - трапеция
АС - диагональ трапеции
AB = CD - боковые стороны
АС ⊥ CD
AD = 40√3 м - большее основание
∠A = ∠D = 60°
Найти:
S - площадь трапеции
Рассмотрим прямоугольный треугольник ACD, гипотенуза которого AD = 40√3 м и ∠D = 60°.
Катеты АС и CD этого треугольника равны
АC = AD · sin 60° = 40√3 · 0.5√3 = 60 (м)
CD = AD · cos 60° = 40√3 · 0.5 = 20√3 (м)
Поскольку трапеция равнобедренная, то
АВ = CD = 20√3 м.
Из вершины С прямого угла треугольника ACD опустим на гипотенузу AD высоту CK, которая одновременно является и высотой трапеции
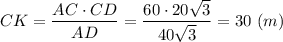
В треугольнике ACD
∠CAD = 90° - ∠D = 90° - 60° = 30°
Основания трапеции ВС ║ АD
∠ACB = ∠CAD = 30° (внутренние накрест лежащие углы при ВС ║ АD и секущей АС).
Рассмотрим ΔАВС.
∠ВАС = ∠BАD - ∠CAD = 60° - 30° = 30°
Поскольку в ΔАВС углы ∠ВАС = ∠ACB = 30°, то ΔАВС - равнобедренный, то есть ВС = АВ = 20√3 м.
Площадь трапеции равна произведению полусуммы оснований на высоту.
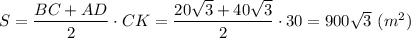
1*1см=1квадратний сантиметр