Как ни удивительно, но в данном случае формула Герона для площади - это самый простой вычисления синуса большего угла. К сожалению, этот треугольник нельзя разрезать на Пифагоровы.
Первое, что надо понять - все размеры можно смело сократить на 5. В этом случае получается треугольник со сторонами 8, 15, 21, подобный исходному, то есть у него - такие же точно углы. Нужно найти угол противолежащий стороне 21(против большей стороны лежит больший угол). Обозначим его Ф.
Надем площадь.
Полупериметр (8 + 15+ 21)/2 = 22; 22 - 8 = 14; 22 - 15 = 7; 22 - 21 = 1;
S^2 = 22*14*7*1 = 11*14^2; S = 14*корень(11);
Поскольку S = 8*15*sin(Ф)/2, то sin(Ф) = (7/30)*корень(11);
С другой стороны, для cos(Ф) можно записать теорему косинусов
21^2 = 8^2 + 15^2 - 2*8*15*cos(Ф);
Откуда cos(Ф) = (21^2 - 8^2 - 15^2)/240 = 19/30;
Поскольку оба результата на первый взгляд получены разными можно проверить, что
(sin(Ф))^2 + (cos(Ф))^2 = 1; сделайте это сами :)
ответ.
ΔАВС , точки Д , К М - точки касания вписанной окружности сторон треугольника , АД=ДС , cosC=2/3 , ВC=9 . Найти r .
Так как АД=ДС , то ΔАДС - равнобедренный . Проведём в нём высоту ДН . Тогда АН=НС . Обозначим АН=НС=х , тогда АС=2х .
И найдём ДС .
ДС=х/cosC=3x/2
Так как отрезки касательных, проведённых из одной точки к окружности равны, то КС=ДС=3х/2 .
Аналогично, ВД=ВМ и АК=АМ .
ВД=ВС-ДС=9-3х/2 , АК=АС-КС=2х-3х/2=х/2
АВ=АМ+ВМ=х/2+(9-3х/2)=9-х
Применим теорему косинусов к ΔАВС .
Значение 0 не подходит по смыслу . Значит, х=2 .
Стороны треугольника равны
Известна формула площади треугольника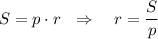
Полупериметр треугольника равен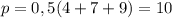
Площадь треугольника по формуле Герона равна
Радиус вписанной окружности равен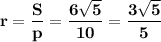 .
.