30° и 60°
Объяснение:
1) Пусть О - точка пересечения диагоналей трапеции.
ΔВОС подобен ΔАОD, при этом коэффициент подобия k равен:
k = AD : ВС = 2 : 1 = 2, т.к., согласно условию, АD = 2BC.
2) Из подобия треугольников следует, что точкой О:
а) диагональ ВD делится на 2 отрезка:
ВО = BD : 3 = 3√3 : 3 = √3
ОD = BD : 3 · 2 = 3√3 : 3 · 2 = 2√3 ;
б) диагональ АС делится на 2 отрезка:
СО = АС : 3 = 3 : 3 = 1
АО = 3 : 3 · 2 = 2.
3) Так как BD⊥АС, то треугольники ВОС и АОD - прямоугольные.
tg∠CBD = СО : ВО = 1/√3 = √3/3
∠CBD = arctg (√3/3) = 30°
∠ВСА = 90° - ∠CBD = 90° - 30° = 60°.
∠ВDА = ∠CBD = 30° - как углы внутренние накрест лежащие;
∠DАС = ∠ВСА = 60° - как углы внутренние накрест лежащие.
ответ: диагонали трапеции образуют с её основаниями углы 30° и 60°.
Высота правильной четырёхугольной пирамиды равна 12 см, а сторона основания равна 24 см. Вычисли двугранный угол при основании.
——————————————————
Основание правильной четырехугольной пирамиды – квадрат.
Все боковые грани правильной пирамиды образуют с плоскостью основания равные углы, а высота проходит через центр основания, который является центром вписанной и описанной около основания окружностей.
Двугранный угол здесь образован радиусом вписанной окружности и апофемой, как отрезками. перпендикулярными ребру основания в одной точке (по т. о трех перпендикулярах).
Радиус вписанной в квадрат окружности равен половине его стороны.
r=24:2=12 (см)
Соединив основание апофемы с центром основания ( основанием высоты пирамиды), получим прямоугольный треугольник.
При этом катеты- высота пирамиды и половина стороны основания - равны 12 см.
Следовательно, треугольник - равнобедренный. Острые углы равнобедренного прямоугольного треугольника равны 45º.⇒ Искомый угол равен 45º.
Объяснение:
cosα = ±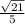
tg α = ±2/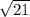 , ctg
, ctg 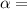 ±
±