Дано :
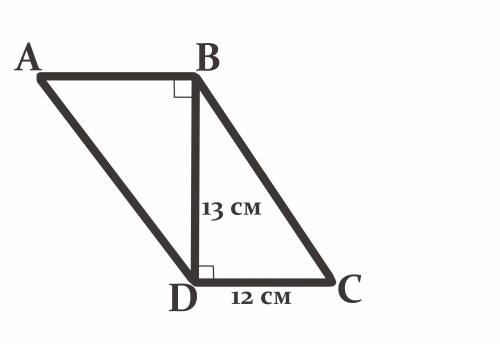
Четырёхугольник ABCD - параллелограмм.
Отрезок DB - диагональ = 13 см.
∠ABD = 90°.
CD = 12 см.
Найти :
S(ABCD) = ?
AB ║ CD (по определению параллелограмма).
Рассмотрим накрест лежащие ∠ABD и ∠BDC при параллельных прямых АВ и CD и секущей BD.
При пересечении двух прямых секущей накрест лежащие углы равны.То есть -
∠ABD = ∠BDC = 90°.
Тогда отрезок BD - ещё и высота параллелограмма ABCD (по определению).
Площадь параллелограмма равна произведению его стороны и высоты, опущенной на эту сторону.Следовательно -
S(ABCD) = BD*CD
S(ABCD) = 13 см*12 см
S(ABCD) = 156 см².
156 см².
Докажите что АВСD параллелограмм если: А(6;-1); В(9;0); С(10;-2); D(7;-3)
Объяснение:
По признаку параллелограмма нужно чтобы противоположные стороны были равными.
АВ=√( (9-6)²+(0+1)²)= √( 3²+1²)=√10.
ВС=√( (10-9)²+(-2-0)²)= √( 1²+(-2)²)=√5.
CD=√( (7-10)²+(-3+2)²)= √( 9+1)=√10.
DА=√( (6-7)²+(-1+3)²)= √( 1²+(2)²)=√5.
Получили АВ= CD , ВС=DА , значит АВС D- параллелограмм.