Дано:
АВСД- пар-м.
ВК- биссектриса угла В
АК - АД = 1 см
Р(периметр) = 40 см.
Найти:
Стороны пар-ма
1) Рассмотрим треугольник АВК - он равнобедренный (по свойству о биссектрисе, проведённой в параллелограмме)
в нём:
АК = АВ (т.к боковые стороны)
2) Пусть КД - Х см. , тогда АК - Х=1 , а т.к АК = АВ (по выше доказанному), следовательно АВ - тоже Х+1, а т.к в параллелограмме все стороны попарено параллельны, то ВС - 2Х+1, а СД - Х +1, а т.к сумма всех сторон равна 40 см. (по условию), то составим уравнение:
Х + Х + 1 + Х + 1 + 2Х + 1 + Х + 1 = 40
Дальь ше решаешь уравнение и находишь оставшиеся стороны алгебрачиски. Всё, и ответ будет готов.
смотри ниже
Объяснение:
2. уравнение прямой: y=kx+C; Эта прямая пересекает ось 0Y в точке C, а тангенс угла между этой прямой и осью 0X равен k.
Если прямая параллельна оси 0X, то угол между прямой и этой осью равен нулю. Тангенс нуля тоже равен нулю, значит k=0. Получаем уравнение прямой, параллельной оси 0X: y=0*x+C; то есть y=C
Значит в задании 2. уравнение прямой имеет вид y=-2
3. подставляем значение абсциссы (x=1) в уравнение и находим нужные точки.
Первая точка (1;4) вторая (1;-4)
4. уравнение окружности
Где (a;b) координаты центра окружности.
В данном уравнении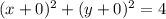
центр окружности находится в начале координат (0;0), значит наша прямая совпадает с осью 0Y и описывается уравнением x=0
5. прямая y=8 параллельна оси абсцисс 0X, значит диаметр окружности равен 8, а радиус равен 4.