9 м.
Объяснение:
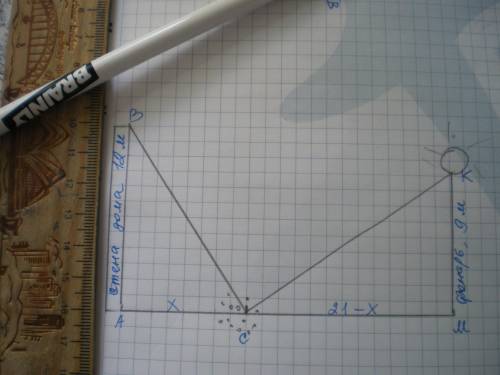
Расстояние от крыши дома до зёрен и от фонаря до зерен представляет собой гипотенузы прямоугольных треугольников АВС и КМС, как показано на рисунке. Если голуби при одинаковой скорости подлетели к корму одновременно, значит, эти гипотенузы равны, ВС=СК.
АВ - стена дома, МК - фонарь. АВ=12 м, МК=9 м.
Пусть искомое расстояние от дома до зерен АС=х м, тогда расстояние от основания столба до зерен СМ=21-х м.
По теореме Пифагора имеем равенство
ВС²=12²+х², а СК²=9²+(21-х)²
Поскольку ВС=СК, равенство принимает вид
12²+х²=9²+(21-х)²
144+х²=81+441-42х+х²
42х=378
х=9.
Расстояние от дома до зёрен 9 м.
ответ: 5 (метров)
Объяснение: Обозначим высоту дома АВ, высоту фонаря МЕ, расстояние между домом и фонарем АМ ( см. рисунок), место, где лежат зерна, обозначим С.
Т.к. и дом, и фонарь перпендикулярны земле, соединив точки В и Е с точкой С, получим прямоугольные треугольники АВС и СЕМ, гипотенузы которых равны (так как голуби летели с равными скоростями и прилетели одновременно к зерну).⇒ ВС=СЕ
Примем АС=х, тогда СМ=17-х.
ВС²=ВА²+АС²
ЕС²=СМ²+ЕМ²
ВА²+АС²=СМ²+ЕМ²
12²+х²=(17-х)²+5², ⇒ 34х=170, х=5 (метров) = расстояние от дома до зерна.

Відповідь:
трикутник прямокутний.
Пояснення:
А(7;4;5) В(4;2;1) С(2;1:3)
Для того, щоб вияснити чи трикутник прямокутний, потрібно:
1) обчислити сторони трикутника;
2) перевірити, чи виконується умова т.Піфагора.
1) |AB|=√((4-7)²+(2-4)²+(1-5)²)=√((-3)²+(-2)²+(-4)²)=√(9+4+16)=√29;
|BC|=√((2-4)²+(1-2)²+(3-1)²)=√((-2)²+(-1)²+2²)=√(4+1+4)=√9=3;
|AC|=√((2-7)²+(1-4)²+(3-5)²)=√((-5)²+(-3)²+(-2)²)=√(25+9+4)=√38
2) Так як у прямокутного трикутника гипотенузою є більша сторона, то припустимо, що АС - гіпотенуза, тоді АВ и ВС - катети. Перевіримо чи діє т.Піфагора:
АС²=АВ²+ВС².
(√29)²+3²=29+9=38=АС²⇒АС=√38.
Відповідь: трикутник прямокутний.