Во первых, хорда не должна превышать размера диаметра окружности. Сначала нужно с циркуля измерить длину отрезка, потом совместить с диаметром окружности, не изменяя раствора циркуля. В случае, если второй конец циркуля выходит за пределы окружности, задача не имеет решения.
Во-вторых, если вышеуказанное не выполнилось, то надо совместить первую ножку циркуля, не меняя раствор циркуля, с любой точкой на окружности, а второй ножкой циркуля подобрать другую точку на окружности. Вообще-то, если отрезок меньше диаметра окружности, то получатся две искомые точки, или два отрезка. В случае же, когда отрезок равен диаметру точки В и С совпадают.
Вот и все.
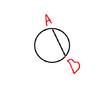
Во первых, хорда не должна превышать размера диаметра окружности. Сначала нужно с циркуля измерить длину отрезка, потом совместить с диаметром окружности, не изменяя раствора циркуля. В случае, если второй конец циркуля выходит за пределы окружности, задача не имеет решения.
Во-вторых, если вышеуказанное не выполнилось, то надо совместить первую ножку циркуля, не меняя раствор циркуля, с любой точкой на окружности, а второй ножкой циркуля подобрать другую точку на окружности. Вообще-то, если отрезок меньше диаметра окружности, то получатся две искомые точки, или два отрезка. В случае же, когда отрезок равен диаметру точки В и С совпадают.
Вот и все.

Відповідь:
Рисуй ABCD угол С- тупой, бок. стороны равны. Проведи диагональ АС. т.к. углы ВСА= АСД , но ВСА=САД, тогда углы САД и АСД равны, значит, треугольник АСД - равнобедренный с основанием АС и боковыми сторонами АД и СД.
СД=АД=20 опусти высоту СН к АД, НД=(20-14)/2=3 СД=20, найдем СН по т. Пифагора.
СН=√391
S=(14+20)/2*√391=17√391
Пояснення: