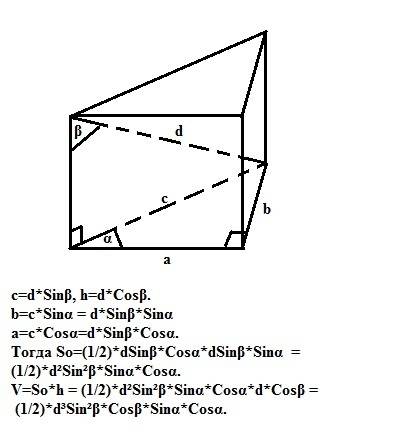
Объем прямой призмы равен произведению площади основания на высоту. V = So*h. В нашем случае площадь основания - это площадь прямоугольного треугольника So=(1/2)*a*b, где а и b - катеты. Для начала найдем гипотенузу "с" основания и высоту призмы "h" из прямоугольного треугольника, образованного диагональю большей боковой грани "d" (как гипотенуза): так как Sinβ =c/d, a Cosβ=h/d, то
с=d*Sinβ, h=d*Cosβ.
В прямоугольном треугольнике (основание призмы) Sinα=b/c, Cosα=a/c. Отсюда катеты равны
b=c*Sinα = d*Sinβ*Sinα и a=c*Cosα=d*Sinβ*Cosα.
Тогда So=(1/2)*dSinβ*Cosα*dSinβ*Sinα =(1/2)*d²Sin²β*Sinα*Cosα.
V=So*h = (1/2)*d²Sin²β*Sinα*Cosα*d*Cosβ = (1/2)*d³Sin²β*Cosβ*Sinα*Cosα.
Дано:
∠MOH = ∠POH ; Луч НО – биссектриса ∠MHP .
∠MHO =∠PHO = (1/2)*∠MHP - - - - - - - - - - - - - - - - - - - -
1) Док -ать Δ MOH = Δ POH
- - - - - - - - - - - - - - - - - - - -
2) дополнительно : ∠MHO = 42⁰, ∠HMO = 28⁰, ∠НОМ = 110⁰. - - - - - - - - - - - - - - - - - - - -
Найти: ∠OHP - ? ; ∠HPO ; ∠НОР . * * *∠OHP ≡∠PHO * * *
|| ∠OHP - ? ; ∠HPO-? ∠НОР - ? ||
* * * ∠НОМ = 180°-(∠MHO+∠HMO) = 180°-(28⁰ +42⁰) =180°- 70⁰=110⁰
! Второй признак равенства треугольников :
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, такие треугольники равны.