Объяснение:
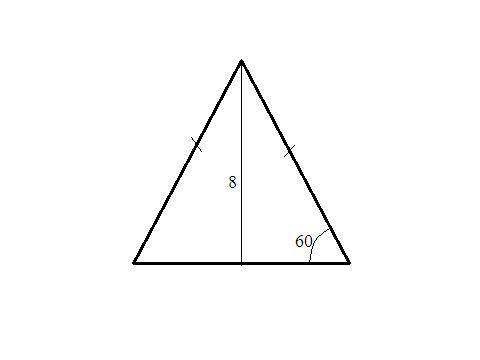
Осевое сечение конуса - равнобедренный треугольник с боковыми сторонами (образующие конуса), основание - диаметр основания.
Треугольник, образованный высотой, образующей и половиной диаметра - прямоугольный. Угол при вершине (90-60)=30° ⇒ половина диаметра (катет против угла 30°) равен половине образующей (гипотенуза). По т. Пифагора -
(2х)²=8²+х²
х²=8²/3
х=8/√3;
Площадь - S=a*h/2, где а=2х=16/√3, h=8;
S=16*8/(2√3)=64/√3=64√3/3.
Можно проще.
Угол при основании 60° ⇒ треугольник равносторонний.
S=h²/√3=8²/√3=64/√3=64√3/3.
Окружность описана, значит суммы ее противоположных сторон равны. Т.е. сумма боковых сторон равна сумме оснований. Так как трапеция равнобедренная то боковые стороны равны. Значит сумма боковых сторон равна сумме оснований равна 5+5=10 см.
Так как угол равен 30. То катет лежащий против нее равен половине гипотенузы, катетом будет высота трапеции, а гипотенузой боковая сторона. Значит высот равна 5:2=2,5 см.
Площадь трапеции равна произведению половине суммы оснований на высоту, значит: 10:5*2,5=12,5 кв.см
Объяснение:
тупоугольный
Объяснение: