В равнобедренном треугольнике ABC угол B равен 110 градусов. Определите угол между прямой, содержащей высоту AA1, и прямой, содержащей биссектрису BB1. ответ запишите в градусах.
Объяснение:
Высота АА₁ падает на продолжение стороны ВС, т.к ∠АВС тупой. Тогда углом между между прямой, содержащей высоту AA₁, и прямой, содержащей биссектрису BB₁ будет∠АОВ₁ .
Угол АВС внешний для Δ АВА₁, значит ∠ВАА₁=110°-90°=20°.
ΔАВС-равнобедренный, углы при основании равны
∠ВАС=(180-110°):2=35° → ∠В₁АО=35°+20°=55°.
Δ АОВ₁ -прямоугольный , ∠АОВ₁=90°-55°=35°
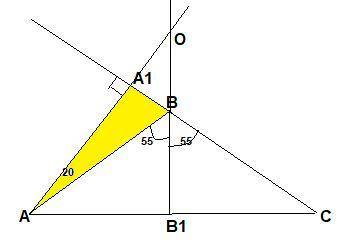
Чертёж смотрите во вложении.
Дано:
ABCD - параллелограмм.
CF - высота, опущенная из вершины ∠BCD на продолжение стороны AD.
ВЕ - высота, опущенная на сторону DC = 8.
DC (меньшая сторона) = 9.
AD (большая сторона) = 12.
Найти:
CF = ?
Площадь параллелограмма равна произведению стороны и высоты, опущенной на эту сторону.
В нашем случае -
S(ABCD) = DC*BE
S(ABCD) = 9*8
S(ABCD) = 72.
Но также формулу площади параллелограмма можно записать так -
S(ABCD) = СF*AD
Выразим через эту формулу значение CF -
CF = S(ABCD)/AD
Подставим в формулу известные нам значения -
CF = 72/12
CF = 6.
ответ: 6 (ед.измерения).