Sромба=ah
проведём из точки B к AD высоту, поставим точку H(у вас наверное по другому формулируют, или вообще не требуют такое писать)
Если BH - высота, то уголBHA=уголBHD=90(градус).(вместо слова угол рисуй уголок).
Рассмотрим треугольник ABH.
УголBAH=60(градусов)(по условию)(в дано записано должно быть).
уголBHA=90(градусов)
сумма углов в треугольнике=180(градусов)
Значит, угол ABH=180-60-90=30(градусов)
В прямоугольном треугольнике, сторона лежащая против угла в 30 градусов равна половине гипотенузы.Значит,
AH=1/2AB
AH=8/2=4
По теореме Пифагора:В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Тогда AB(квадрат)=AH(квадрат)+BH(квадрат)
BH(квадрат)=AB(квадрат)-AH(квадрат)
BH(квадрат)=8(квадрат)-4(квадрат)
BH(квадрат)=64-16
BH(квадрат)=(корень)48
BH=(корень)3 · 16
BH=4·√3
S=ah
S=8·4√3
S=32√3
Я не уверен в ответе, изучаете ли вы корни...Если ответ неуместен, но облом.
Вариант 1
№1. Проведем AD — перпендикуляр к плоскости α. АВ и АС — проекции наклонных DB и DC на плоскость α. Треугольники DAB и DAC — прямоугольные. Так что DC = а : sin45° = a√2 ; DB = а : sin30° = 2a.
Далее, ΔBDC — прямоугольный (по условию). Тогда по теореме Пифагора: BC =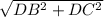 =
= 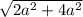 =
= 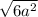 =
= 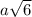
№2. Пусть D - данная точка. DB и DC - наклонные. Проведем AD — перпендикуляр к плоскости α. Тогда АВ и АС — проекции наклонных на плоскость α. Тогда ΔABD и ΔACD — прямоугольные, равнобедренные. Так что АВ = АC = AD = а.
DC = DB = a : sin45 =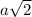
Так что ΔBDC — равнобедренный, а поскольку ∠BDC = 60°, то значит треугольник BDC — равносторонний, т.е.
DB = DC = BC =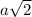
(Дальше долко)