Відповідь:
Пояснення:
Пусть О-точка пересечения диагоналей
А1, В1, С1, Д1, О1 проекции соответствующих вершин и точки пересечения на плоскость
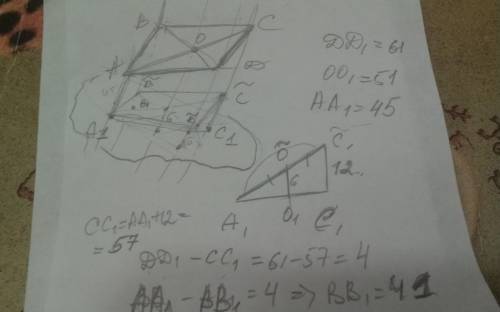
Пусть АА1=45; ДД1=61 и ОО1=51
Сделаем паралельний перенос паралепипеда таким образом, чтоби одна вершина, с наименьшим растоянием к плоскости, ледала на плоскости А1
Тогда рассмотрим △А1С~С1, прямая О~О1 - средняя линия етого △, так как при любой проекции сохраняются соотношение паралельних прямих, → С~С1=2О~О1
О~О1=ОО1-АА1=6 → С~С1=12 → СС1=АА1+12=57
Так как АВ||СД → С~Д~||А1В~ → ДД1-СС1=4
АА1-ВВ1=4→ ВВ1=45-4=41
8 12 16 это 3 средние линии
Объяснение:
почему вы удалили мой ответ, в задаче просили 3 средние линии и я их нашел
я поступил так, если треугольник. из средних линий имеет периметр 36, то он основном треугольник имеет периметр 72, так как маленький сформирован из его средних линий, а они в 2 раза меньше оснований, тобишь сторон большого.
а далее складываем отношения сторон большого треуг. и называем и х, далее 18х=72, получаем х=4
находим стороны
6*4 = 24
4*4 = 16
8*4 = 32
и делим все на 2, ведь нам нужны средние линии
чтд