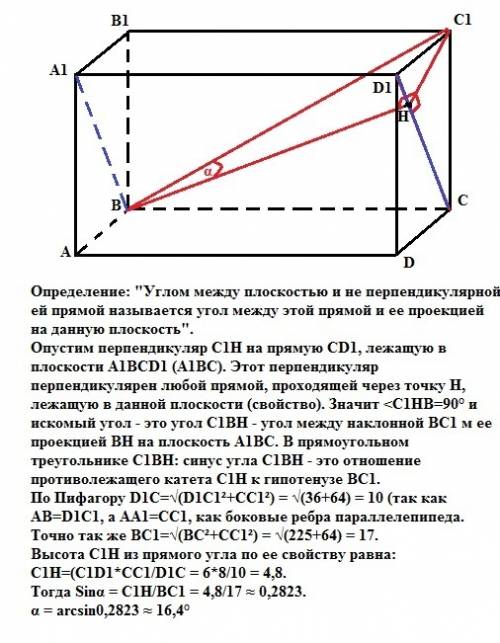
Определение: "Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость".
Опустим перпендикуляр С1Н на прямую СD1, лежащую в плоскости А1ВС (это плоскость А1ВСD1, так как секущая плоскость пересекает параллельные плоскости АА1В1В и DD1C1C по параллельным прямым А1В и D1C). Отрезок С1Н перпендикулярен любой прямой, проходящей через точку Н, лежащую в данной плоскости (свойство). Значит <C1HB=90° и искомый угол - это угол С1ВН - угол между наклонной ВС1 м ее проекцией ВН на плоскость А1ВС. В прямоугольном треугольнике С1ВН: синус угла С1ВН - это отношение противолежащего катета С1Н к гипотенузе ВС1.
По Пифагору D1C=√(D1C1²+CC1²) = √(36+64) = 10 ед (так как АВ=D1C1, a AA1=CC1, как боковые ребра параллелепипеда.
Точно так же ВС1=√(ВC²+CC1²) = √(225+64) = 17 ед.
Высота С1Н из прямого угла по ее свойству равна:
С1Н=(С1D1*CC1/D1C = 6*8/10 = 4,8 ед.
Тогда Sinα = C1H/BC1 = 4,8/17 ≈ 0,2823.
α = arcsin0,2823 ≈ 16,4°.
Есть 2 метода решения.
1) По формуле Герона.
Находим длины сторон треугольника.
AB = √((xB-xA)²+(yB-yA)²+(zB-zA)²) = 1 4 9 14 3,741657387 c
BC = √((xC-xB)²+(yC-yB)²+(zC-zB)²) = 4 4 4 12 3,464101615 a
AC = √((xC-xA)²+(yC-yA)²+(zC-zA)²) = 9 0 1 10 3,16227766 b
Периметр АВС Р = 10,36803666 p - a p - b p - c
Полупериметр р= 5,184018331 1,719916716 2,021740671 1,442360944
S = √26 = 5,099019514.
Далее по теореме косинусов находим:
cos A = 0,507092553 cos B = 0,6172134 cos C = 0,365148372
A = 1,03898823 В = 0,905600272 С = 1,197004152 радианы
59,52964053 51,8870735 68,58328597 градусы
.
2) По векторам.
ВА = (-1; 2; -3), модуль √14
ВС = (2; 2; -2), модуль √12.
ВАхВС = -2 + 4 + 6 = 8.
cos B = 8/(√14*√12) = 0,617213.