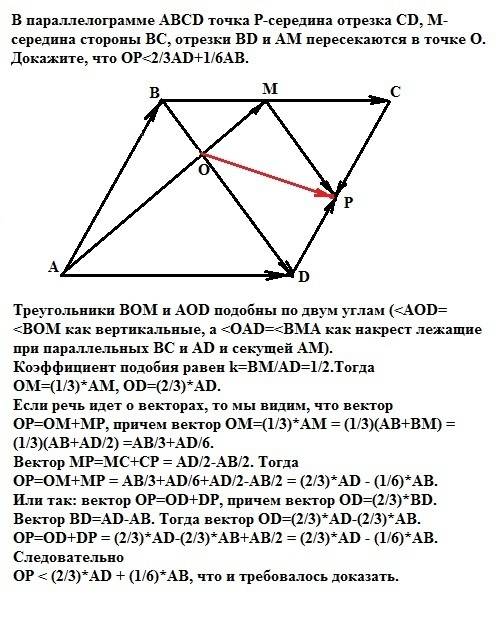
Треугольники ВОМ и AOD подобны по двум углам (<AOD=<BOM как вертикальные, а <OАD=<BMА как накрест лежащие при параллельных ВС и AD и секущей АМ). Коэффициент подобия равен k=BM/AD=1/2. Тогда ОМ=(1/3)*АМ, OD=(2/3)*AD.
Если речь идет о векторах, то мы видим, что вектор ОР=ОМ+МР, причем вектор ОМ=(1/3)*АМ = (1/3)(АВ+BM) = (1/3)(АВ+AD/2) =AB/3+AD/6. Вектор MP=MC+CP = AD/2-AB/2. Тогда
ОР = ОМ+МР = AB/3+AD/6+AD/2-AB/2 = (2/3)*AD - (1/6)*AB.
Или так: вектор ОР=ОD+DР, причем вектор ОD=(2/3)*BD.
Вектор BD=AD-AB. Тогда вектор OD=(2/3)*AD-(2/3)*AB.
ОР = ОD+DР = (2/3)*AD-(2/3)*AB+AB/2 = (2/3)*AD - (1/6)*AB.
Следовательно
ОР < (2/3)*AD + (1/6)*AB, что и требовалось доказать.
a) K, L, M ∈ α; α║(SBC)
KL║BS; KM║BC; ML║CS как линии пересечения двух параллельных плоскостей с одной общей.
SH⊥(ABC); AT⊥BC; H∈AT как центр правильного треугольника лежащий на медиане. AH:HT=2:1 по свойству пересечения медиан.
LU⊥KM ⇒ KU=UM ⇒ U∈AT ⇒ LU⊂(AST) ⇒ LU∩SH
Рассмотрим плоскость AST.
LU║ST как линии пересечения двух параллельных плоскостей с (AST).
AK:KB=AL:LS=5:1 по теореме о пропорциональных отрезках.
AU:UT=AL:LS по теореме о пропорциональных отрезках.
Как уже известно AH:HT=2:1. Пусть AU=5x; UT=x ⇒AT=6x ⇒ AH=4x; HT=2x ⇒ HU=2x-x=x.
ΔSHT~ΔRHU по 3 углам (1 общий остальные равны как соответственных угла при параллельных прямых).
Значит SH:RH=HT:HU=2:1. Пусть SH=2y; RH=y ⇒ SR=2y-y=y ⇒ SR=y=RH
То есть плоскость делит высоту пополам.
б) AT=AB*sin 60°=(15+3)*√3/2=9√3.
ΔAST~ΔALU по 3 углам (1 общий остальные равны как соответственных угла при параллельных прямых).
Значит AL:AS=LU:ST=6:5.
HT=1/3 *9√3=3√3 т.к. AH:HT=2:1
SH=13 ⇒ ST=√(169+27)=14 ⇒ LU=5/6 *14=35/3.
ΔAKM~ΔABC по 3 углам (1 общий остальные равны как соответственных угла при параллельных прямых).
Значит KM:BC=AK:AB=5:6 ⇒ KM=5/6 *18=15.
Как было указано в начале LU⊥KM ⇒ S=1/2* 15*35/3=175/2=87,5
ответ: 87,5.