Для решения применим теорему Фалеса: Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
Чтобы без линейки с делениями разделить отрезок, длина которого не известна, нужно от одного из концов этого отрезка провести под углом к нему вс луч и на этом луче на равном расстоянии отметить нужное количество точек.
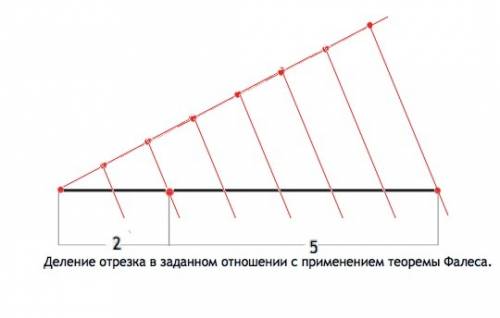
а) На вс луче отложим через равные промежутки 2+5 =7 точек. Затем через последнюю точку и конец заданного отрезка проведём прямую и через все точки ещё 6 прямых, параллельных ей. При этом заданный отрезок будет разделен на 7 равных частей. Отсчитаем 2 из получившихся отрезков. Остальная часть равна 5 отмеренным отрезкам, а исходный разделен в отношении 2:5
Можно на заданном отрезке откладывать не 7 отрезков, а провести всего 2 прямые - через седьмую и параллельно ей через вторую точку. Заданный отрезок будет разделён в нужном отношении.
б) и в) делим точно так же.
Основанием конуса будет большее сечение шара, так как радиус основания конуса равен радиусу шара по условию. Значит, высота конуса тоже равна радиусу шара.
Объем конуса находят по формуле:
V = ⅓ * π * R ² * h, где R - радиус основания, h - высота конуса.
Так как высота конуса равна радиусу шара формула примет вид:
V = ⅓ * π * R ³.
Объем шара: V = (4 * π * R ³) / 3. V = 36 ( по условию )
36 * 3 = 4 * π * R ³
108 = 4 * π * R ³
π * R ³ = 27.
Подставим значение π * R ³ в формулу объема конуса:
V = ⅓ * 27 = 9.