Пусть AK и CM – медианы и точка О – точка их пересечения
Медианы в точке пересечения делятся в отношении 2:1, считая от вершины.
Пусть АО=СО=2х, тогда ОК=ОМ=х
Из прямоугольного равнобедренного треугольника АОС по теореме Пифагора будем иметь:
25=4x^2+4x^2 => 8x^2=25 => x^2= 25/8 => x=5/sqrt(8)
OK=OM=5/sqrt(8)
Из вершины В треугольника проведем медиану ВН, тогда из треугольника АОН находим ОН:
ОН^2=OA^2-AH^2
OH=sqrt(100/8-25/4)=sqrt(25/4)=5/2
Площадь треугольника AOH равна
S=1/2*AH*OH=1/2*5/2*5/2=10/8
Площадь треугольника ABC равна
S1=6*S=6*10/8=30/4=7,5
1.Призма ABCA'B'C' , AB=AC=3 ; BC=2.Опустим перпендикуляр из точки B', который падает за пределы основания в точку K, на продолжение прямой AB.Тогда в прямоугольном треугольнике BB'K угол K прямой и угол B' = 45.
B'K=h - высота призмы.h=sin 45 *BB'=2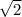 .
.
S - площадь основания.Т.к. треугольник равнобедренный, то проведём перпендикуляр из вершины A к основанию BC в точку F(будет являться высотой, медианой),
тогда BF=FC=1
AF=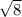
S=1/2*AF*FC*2=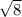
V=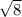 *2*
*2*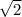 =8
=8
V куба = 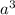 =8
=8
a=2 ответ: ребро куба равно 2
3.
Прямоугольный треугольник со сторонами a, b ,c-гипотенуза.
S-площдь основания
S=1/2*a*b=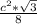
a=sin 30*c
b=cos 30*c
H=sin 60*k
V=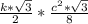
12
Объяснение:
Против угла 30 градусов лежит катет, равный половине гипотенузы. Значит гипотенуза равна 6*2=12