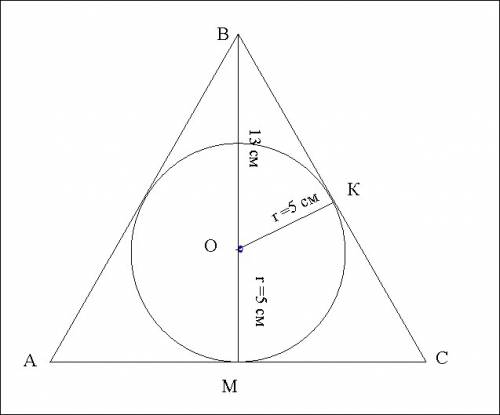
Дано: ΔАВС
АВ=ВА
(О; r) - вписанная окр.
ВМ⊥АС
ВО=13 см
ОК= r = 5 см
Найти: Р ΔАВС
1) Из прямоугольного ΔВОК по теореме Пифагора
ВК² = ВО² - ОК²
ВК² = 13²- 5² =169-25=144
ВК=√144 = 12 см
2) ∆ОВК~∆МВС (подобен), т.к. оба прямоугольные с общим углом ∠МВС.
Соответственные стороны пропорциональны:
ВМ : МС = ВК : ОК
18 : МС = 12 : 5
МС =18 · 5:12 = 7,5 см
АС = 2 · МС = 2·7,5 = 15 см.
3) По теореме Пифагора из ∆ВМС найдем ВС.
ВС² = ВМ² + МС²
ВС² = 18² + 7,5² = 324 + 56,25 = 380,25
ВС=√380,25 = 19,5 см
4) АВ = ВС = 19,5 см
АС = 15 см
Р= АВ+ВС+АС
Р = 2*19,5 + 15 = 54 см
ответ: 54 см
Площадь прямоугольника
S=a×b=8×15=120см²
Объяснение: диагональ делит прямоугольник на две равных между собой прямоугольных треугольников. У которых диагональ прямоугольника является гипотенузой, а стороны прямоугольника катетами прямоугольного треугольника.
Диагональ d=17см= гипотенуза
Сторона а=8см=катет
По теореме Пифагора
a²+b²=c² a и b катеты , с гипотенуза
Неизвестный сторона b прямоугольника
b=√(с²-а²)
b=√(17²-8²)= √(289-64)=√225=15см