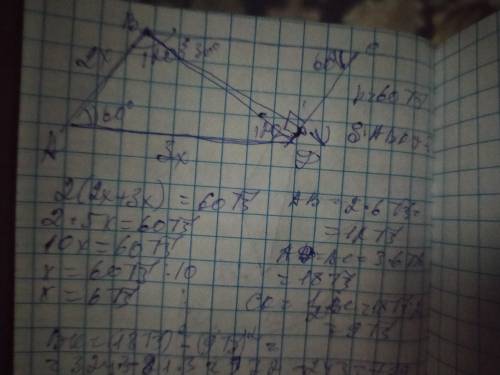
Обозначим эти пропорции как 2х и 3х. Зная периметр параллелограмма составим уравнение:
2(2х+3х)=60√3
2×5х=60√3
10х=69√3
х=60√3/10
х=6√3
Тогда АВ=СД=2×6√3=12√3
ВС=АД=3×6√3=18√3
Высота ВК делит параллелограмм, образуя прямоугольный треугольник ВСК. В нём ВК и СК - катеты, а ВС - гипотенуза. Так как сумма односторонних углов параллелограмма составляет 180°, то угол С=180-120=60°
Сумма острых углов прямоугольного треугольника составляет 90°, поэтому угол СВК=90-69=30°. Катет лежащий напротив него равен половине гипотенузы, поэтому
СК=½×ВС=18√3/2=9√3
Найдём ВК по теореме Пифагора:
ВК²=ВС²-СК²=(18√3)²-(9√3)²=324×3-81×3=
=972-243=729; ВК=√729=27
ВК=27
Найдём S∆ВСК по формуле: S=½×BK×CK=
=½×9√3×27=121,5√3
Теперь найдём площадь параллелограмма по формуле:
S=СД×ВК=12√3×27=324√3
Теперь найдём площадь четырёхугольника АВКД:
Sавкд=Sпарал–Sвск=
=324√3-121,5√3=202,5√3
ОТВЕТ: Sавкд=202,5√3

Объяснение: в основании правильной четырёхугольной пирамиды лежит квадрат. Его площадь S=a², где а - его сторона. Sосн=10²=100(ед²)
Диагонали квадрата делят его на 2 равных равнобедренных прямоугольных треугольников, и также сами делятся пополам, поэтому АО=СО=ВО=ДО. Рассмотрим полученный ∆АВС, В нём АВ и ВС - катеты, а АМ- гипотенуза. В равнобедренном прямоугольном треугольнике гипотенуза в √2 больше катета, поэтому АС=10√2(ед)
Так как диагонали квадрата делятся пополам, то АО=СО=10√2/2=5√2(ед)
Рассмотрим ∆АОS. В нём АО и SO- катеты, а АS- гипотенуза. Найдём высоту пирамиды SO по теореме Пифагора:
SO²=АS²-АО²=(√59)²-(5√2)²=59-25×2=
=59-50=9; SO=√9=3(ед)
Теперь найдём объем пирамиды зная площадь основания и её высоту по формуле: V=⅓×Sосн×h=⅓×100×3=100(ед³)