1. ∠АВС = 65°.
2. ∠АВС = 115°.
Объяснение:
Расположение точки В нам неизвестно, но предполагаем, что она находится на окружности.
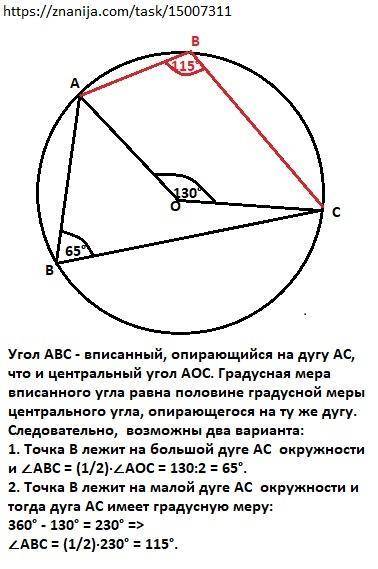
Угол АВС - вписанный, опирающийся на дугу АС, что и центральный угол АОС. Градусная мера вписанного угла равна половине градусной меры центрального угла, опирающегося на ту же дугу. Градусная мера центрального угла равна градусной мере дуги, на которую он опирается.
Следовательно, возможны два варианта:
1. Точка В лежит на большой дуге АС окружности и
∠АВС = (1/2)·∠АОС = 130:2 = 65°.
2. Точка В лежит на малой дуге АС окружности и тогда дуга АС имеет градусную меру:
360° - 130° = 230° =>
∠АВС = (1/2)·230° = 115°.
Первая страница.
Задание 4.
Треугольник прямоугольный.
Пусть ВС=х, тогда гипотенуза АВ=х+2.
По теореме Пифагора в треугольнике АВС:
АВ²= ВС²+АС²;
(х+2)²=х²+(√20)²;
х²+4х+4=х²+20;
4х= 16;
х= 4.
ВС=4, тогда АВ=4+2=6.
ОТВЕТ: 6.
Задание 5.
Итак, АМ=МС=4 => АС=4+4=8.
Треугольник по условию равносторонний с основанием АС. Угол А равен углу С и равен 60° => треугольник равносторонний.
Площадь равностороннего треугольника равна:
S= √3/4 × a², где а - сторона треугольника.
S= √3/4 ×8²= 16√3.
ОТВЕТ: 16√3.
Вторая страница.
Задание 4.
Площадь трапеции равна произведению полусуммы ее оснований на высоту.
Рассмотрим четырехугольник КВСD.
Он — параллелограмм, поскольку по условию ВК||CD, а BC||KD (т.к. это трапеция, а ВС и KD - ее основания)
Значит, ВК=KD=4.
Основание трапеции AD= AH+HK+KD=2+8+4=14.
BK=CD=17.
В ΔВНК (угол ВНК=90°) по т. Пифагора:
ВН²= ВК²-НК²;
ВН²= 17²-8²;
ВН²= 225;
ВН= 15 (-15 не подходит).
По формуле площади трапеции находим ее:
Sabcd= ½(BC+AD)BH;
Sabcd= ½(4+14)×15= 9×15= 135.
ОТВЕТ: 135 см².
Задание 5.
Решение во вложении. Как находить площадь, Вы знаете уже из предыдущей задачи, поэтому сразу подставляла цифры.
