периметр ромба равен 4а.
решение.
меньшая диагональ ромба равна а. это как раз диагональ проведенная из вершины тупого угла и образует с высотой угол 30 град. высота - это перпендикуляр к противоположно стороне ромба (т.е.) образует угол 90 град. т.к. сумма углов треугольника равна 180, то угол между короткой диагональю и стороной ромба равен 60 град. получается, что короткая диагональ делит ромб на 2 равносторонних треугольника и диагональ равна стороне ромба, т.е. а. таким образом периметр равен 4а
Объяснение:
Щоб знайти відстань від центра кулі до площини трикутника, ми можемо використати теорему Піфагора. Теорема Піфагора говорить, що в прямокутному трикутнику квадрат гіпотенузи рівний сумі квадратів катетів. В нашому випадку, ми знаємо, що радіус кулі складає 5 сантиметрів, і це буде наша гіпотенуза. Також ми знаємо, що сторони трикутника складають 15 сантиметрів і 15 сантиметрів, і це будуть наші катети. Тепер ми можемо розв'язати рівняння, щоб знайти відстань від центра кулі до площини трикутника:
h^2 = 5^2 - (15^2 + 15^2) / 2
h^2 = 25 - 225
h^2 = -200
h =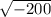
На жаль, коренем з від'ємного числа не може бути, тому ми можемо сказати, що куля не може дотикатися до всіх сторін трикутника. Щоб куля могла дотикатися до всіх сторін трикутника, радіус кулі повинен бути більшим ніж піввисота трикутника.